Question

如图在反比例函数y=-

2

x

和y=

3

x

的图象上分别有A、B两点，若AB∥x轴且OA⊥OB，则

OA

OB

=______．

Answer 1

AB交y轴于C点，如图，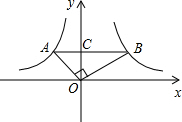
设B点坐标为（a，

3

a

），
∵AB∥x轴，
∴A点的纵坐标为

3

a

，OC⊥AB，
把y=

3

a

代入y=-

2

x

得x=-

2a

3

，则A点坐标为（-

2a

3

，

3

a

），
∵OA⊥OB，
∴∠AOB=90°，
∴Rt△AOC∽Rt△OBC，
∴

OA

OB

=

OC

BC

=

AC

OC

，即

OA

OB

=

3 a

a

=

2a 3

3 a

，
由

3 a

a

=

2a 3

3 a

得a⁴=

27

2

，
∴a²=

3 6

2

，
∴即

OA

OB

=

3 a

a

3

a2

=

3

3 6 2

=

6

3

．
故答案为

6

3

．