Question

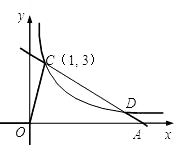
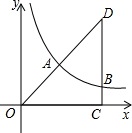
已知：如图，在直角坐标系xOy中，Rt△OCD的一边OC在x轴上．∠C=90°，点D在第一象限，OC=3，DC=4，反比例函数的图象经过OD的中点A．
（1）求该反比例函数的解析式；
（2）若该反比例函数的图象与Rt△OCD的另一边DC交于点B，求过A、B两点的直线的解析式．

Answer 1

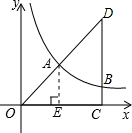
（1）过点A作AE⊥x轴于点E．
∵∠OCD=90°，
∴AE∥CD．A为OD中点，OC=3，DC=4，
∴AE是△OCD的中位线，
∴OE=EC=

1

2

OC，
∴A（1.5，2）；
设反比例函数解析式为y=

k

x

，
那么k=1.5×2=3，
∴y=

3

x

；

（2）当x=3时，y=1，
∴B（3，1）；
设过A、B两点的直线的解析式为y=k₂x+b，
则

2=1.5k2+b 1=3k2+b

，
解得：

k2=- 2 3 b=3

．
∴y=-

2

3

x+3．