题目内容
已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB,AC相交于D点,双曲线y=
(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:
①菱形OABC的面积为80;②E点的坐标是(4,8);③双曲线的解析式为y=
(x>0);④sin∠COA=
.
其中正确的结论有( )个.

| k |
| x |
①菱形OABC的面积为80;②E点的坐标是(4,8);③双曲线的解析式为y=
| 20 |
| x |
| 4 |
| 5 |
其中正确的结论有( )个.
| A.1 | B.2 | C.3 | D.4 |

作DH⊥x轴于H,BG⊥x轴于G,如图,
∵四边形OABC为菱形,
∴菱形OABC的面积=
OB•AC=
×160=80,所以①正确;
∴
DH•OA=菱形OABC的面积的
=
×80,
而A点的坐标为(10,0),
∴
DH×10=
×80,
∴DH=4,
∵OB与AC互相垂直平分,
∴∠ADO=90°,DH为△OBG的中位线,
∴BG=2DH=8,
∴E点的纵坐标为8,
∵∠DOH+∠ODH=∠ODH+∠ADH=90°,
∴∠DOH=∠ADH,
∴Rt△DOH∽Rt△ADH,
∴DH:AH=OH:DH,即DH2=OH•AH,
∵DH=4,AH=OA-OH=10-OH,
∴OH(10-OH)=16,解得OH=8或OH=2(舍去),
∴D点坐标为(8,4),
把D(8,4)代入y=
得k=4×8=32,
∴反比例函数解析式为y=
,所以③错误;
把y=8代入得
=8,解得x=4,
∴E点坐标为(4,8),所以②正确;
CM⊥x轴于M,如图,
∴CM=BG=8,
∵四边形OABC为菱形,
∴OC=OA=10,
在Rt△OCM中,CM=8,OC=10,
∴OM=
=6,
∴sin∠COM=
=
=
,
即sin∠COA=
,所以④正确.
故选C.
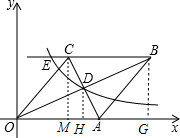
∵四边形OABC为菱形,
∴菱形OABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
而A点的坐标为(10,0),
∴
| 1 |
| 2 |
| 1 |
| 4 |
∴DH=4,
∵OB与AC互相垂直平分,
∴∠ADO=90°,DH为△OBG的中位线,
∴BG=2DH=8,
∴E点的纵坐标为8,
∵∠DOH+∠ODH=∠ODH+∠ADH=90°,
∴∠DOH=∠ADH,
∴Rt△DOH∽Rt△ADH,
∴DH:AH=OH:DH,即DH2=OH•AH,
∵DH=4,AH=OA-OH=10-OH,
∴OH(10-OH)=16,解得OH=8或OH=2(舍去),
∴D点坐标为(8,4),
把D(8,4)代入y=
| k |
| x |
∴反比例函数解析式为y=
| 32 |
| x |
把y=8代入得
| 32 |
| x |
∴E点坐标为(4,8),所以②正确;
CM⊥x轴于M,如图,
∴CM=BG=8,
∵四边形OABC为菱形,
∴OC=OA=10,
在Rt△OCM中,CM=8,OC=10,
∴OM=
| OC2-CM2 |
∴sin∠COM=
| CM |
| OC |
| 8 |
| 10 |
| 4 |
| 5 |
即sin∠COA=
| 4 |
| 5 |
故选C.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 两点,连接OA、OB.
两点,连接OA、OB.



