题目内容
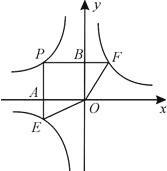
如图,已知点P是反比例函数y=
(k1<0,x<0)图象上一点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交反比例函数y=
(0<k2<|k1|)图象于E、F两点.
(1)用含k1、k2的式子表示以下图形面积:
①四边形PAOB;②三角形OFB;③四边形PEOF;
(2)若P点坐标为(-4,3),且PB:BF=2:1,分别求出k1、k2的值.
| k1 |
| x |
| k2 |
| x |
(1)用含k1、k2的式子表示以下图形面积:
①四边形PAOB;②三角形OFB;③四边形PEOF;
(2)若P点坐标为(-4,3),且PB:BF=2:1,分别求出k1、k2的值.

(1)①S四边形PAOB=|OA|•|OB|=|k1|;
②S三角形OFB=
| 1 |
| 2 |
| 1 |
| 2 |
③S四边形PEOF=S四边形PAOB+S三角形OFB+S△EAO=k2-k1(或k2+|k1|);
(2)因为P(-4,3)在y=
| k1 |
| x |
∴k1=-12;(2分)
又PB:BF=2:1,
∴F(2,3),k2=6(2分)

练习册系列答案
相关题目



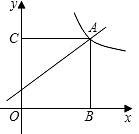 交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C.如果四边形OBAC是正方形,求一次函数的关系式.
交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C.如果四边形OBAC是正方形,求一次函数的关系式.