题目内容
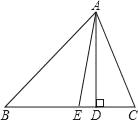
【题目】如图，在Rt△ABC中，∠C=90°，AB=13，AC=12，经过点C且与AB边相切的动圆与BC、CA分别相交于点M、N，则线段MN长度的最小值为 ． 
【答案】
【解析】解：如图，设MN的中点为P，⊙P与AB的切点为D，连接PD，连接CP，CD，则有PD⊥AB；
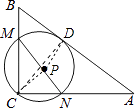
∵AB=13，AC=12，
∴BC= 
=5．
∵PC+PD=MN，
∴PC+PD≥CD，MN≥CD．
∴当MN=CD时，MN有最小值．
∵PD⊥AB，
∴CD⊥AB．
∵ 
ABCD= BCAC，
∴CD= 
= 
= ．
∴CD的最小值 ．
∴MN的最小值为 ．
所以答案是： ．
【考点精析】本题主要考查了切线的性质定理的相关知识点，需要掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题．
练习册系列答案
相关题目
