Question

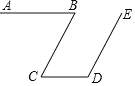
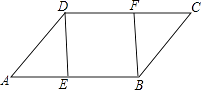
【题目】已知：如图，点、、在同一直线上，、、都是射线，，与互为余角．

（1）与有何关系？请证明你的结论；

（2）与有何关系？请证明你的结论；

（3）与有何关系？请证明你的结论．

Answer 1

【答案】（1），证明见解析；（2），证明见解析；（3），证明见解析．

【解析】

（1）由A、O、E在同一直线上知∠1+∠2+∠3+∠4=180°，又知∠1+∠4=90°，从而推出与互余；

（2）由（1）知∠1+∠4=∠2+∠3，又因为∠1=∠2，则∠3=∠4；

（3）由（2）中∠3=∠4知∠3的补角就是∠4的补角.因为∠4的补角是∠AOD，所以∠3的补角是∠AOD.

（1）与与互余都可以.

证明：∵点、、在同一直线上，

∴，

∵与互为余角，

∴，

∴，

即与互余；

（2）.

证明：由（1）知，，

∴，

又∵，

∴；

（3）与与互补都可以.

证明：由（2）知，

∵点在同一直线上，

∴，

∴，

即与互补.