题目内容
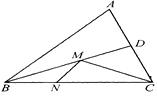
【题目】如图,△ABC是等边三角形,边长为5,D为AC边上一动点,连接BD,⊙O为△ABD的外接圆,过点A作AE∥BC交⊙O于E,连接DE,则△BDE的面积的最小值为 . 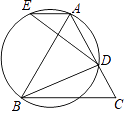
【答案】![]()
【解析】解:如图所示:连接BE, 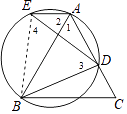
∵等边三角形ABC,
∴∠1=∠C=60°,
∵AE∥BC,
∴∠CAE+∠C=180°,
∴∠CAE=∠1+∠2=180°﹣∠C=120°,
∴∠1=∠2=60°,
∵∠1=4;∠2=∠3(同弧圆周角相等),
∴∠3=∠4=∠1=∠2=60°,
∴△BDE是等边三角形;
当⊙O的半径最小时△BDE的面积的最小,当AB是⊙O的直径时,⊙O的半径最小= ![]() AB=
AB= ![]() ,
,
此时BD⊥AC,
∴DE=BD=ABsin∠1=5× ![]() =
= ![]() ,
,
∴△BDE的面积的最小值= ![]() ×
× ![]() ×
× ![]() ×
× ![]() =
= ![]() .
.
所以答案是 ![]() .
.
【考点精析】掌握等边三角形的性质和三角形的外接圆与外心是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°;过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心.

练习册系列答案
相关题目
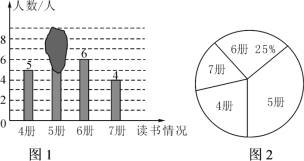
【题目】甲、乙两名工人同时加工同一种零件,现根据两人7天产品中每天出现的次品数情况绘制成如下不完整的统计图和表,依据图、表信息,解答下列问题:
相关统计量表:
量数 人 | 众数 | 中位数 | 平均数 | 方差 |
甲 |
|
| 2 |
|
乙 | 1 | 1 | 1 |
|
次品数量统计表:
天数 人 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
甲 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
乙 | 1 | 0 | 2 | 1 | 1 | 0 |
|
(1)补全图、表.
(2)判断谁出现次品的波动小.
(3)估计乙加工该种零件30天出现次品多少件?