题目内容
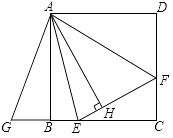
【题目】如图，抛物线y=ax2﹣x+4与x轴交于点A，B，B点的坐标为（﹣4，0），与y轴交于点C．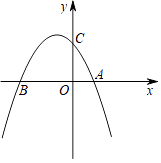
（1）求抛物线的解析式和对称轴．
（2）连接AC、BC，在x轴下方的抛物线上求一点M，使△ABM与△ABC的面积相等．
（3）在x轴下方作平行于x轴的直线l，与抛物线交于点D、E两点（点D在对称轴的左侧）．过点D、E分别作x轴的垂线，垂足分别为G、F，当矩形DEFG中DE=2DG时，求D点的坐标．
【答案】
（1）解：把B（﹣4，0）代入y=ax2﹣x+4得16a+4+4=0，解得a=﹣ 
，
所以抛物线的解析式为y=﹣ x2﹣x+4，
抛物线的对称轴为直线x=﹣ 
=﹣1
（2）解：当x=0时，y=﹣ x2﹣x+4=4，则C（0，4），
∵△ABM与△ABC的面积相等，
∴点M的纵坐标为﹣4，
当y=﹣4时，﹣ x2﹣x+4=﹣4，解得x1=﹣1+ 
，x2=﹣1﹣ ，
∴M点的坐标为（﹣1+ ，﹣4）或（﹣1﹣ ，﹣4）
（3）解：如图，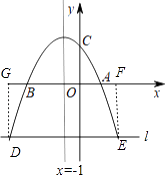 
设D（t，﹣ t2﹣t+4）（t＜﹣1）
∵DE=2DG，
∴﹣1﹣t=﹣（﹣ t2﹣t+4），
整理得t2+4t﹣6=0，解得t1=﹣2﹣ 
，t2=﹣2+ ，
∴D（﹣2﹣ ，﹣1﹣ ）．
【解析】（1）B点在抛物线上，故此点B的坐标符合抛物线的函数解析式，将点B的坐标代入函数关系式可求得a的值；
（2）将x=0代入抛物线的解析式求得对应的y的值，从而可得到点C的坐标，再利用三角形面积公式得到点M、C点到x轴的距离相等，即点M的纵坐标为-4，然后解方程-,x2-x+4=-4即可得到M点的坐标；
（3）设D（t，-t2-t+4）（t＜-1），利用DE=2DG和抛物线的对称性得到关于t的方程，从而可求得t的值，故此可得到点D的坐标.
