题目内容
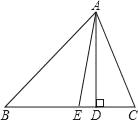
【题目】如图，已知△ABC中，AD⊥BC于点D，AE为∠BAC的平分线，且∠B＝36°，∠C＝66°．求∠DAE的度数．
【答案】16°
【解析】
试题先根据三角形的内角和定理求得∠BAC的度数，再根据角平分线的性质求得∠CAE的度数，由垂直的性质可得∠ABD=90°，再根据三角形的内角和定理求得∠CAD度数，从而可以求得结果.
∵∠B=36°，∠C=66°
∴∠BAC=180°-∠ABC-∠ABC=180°-36°-68°=76°
∵AE为∠BAC的平分线
∴∠CAE=
∠BAC==38°
∵AD⊥BC于D
∴∠ABD=90°
∴∠CAD=180°-∠C-∠ABD=180°-68°-90°=22°
∴∠DAE=∠CAE-∠CAD=38°-22°=16°.
练习册系列答案
相关题目
