题目内容
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
【答案】C
【解析】∵抛物线与x轴的一个交点在点(3,0)和(4,0)之间,而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点在点(﹣2,0)和(﹣1,0)之间.
∴当x=﹣1时,y>0,
即a﹣b+c>0,所以①正确;
∵抛物线的对称轴为直线x=﹣ ![]() =1,即b=﹣2a,
=1,即b=﹣2a,
∴3a+b=3a﹣2a=a,所以②错误;
∵抛物线的顶点坐标为(1,n),
∴ ![]() =n,
=n,
∴b2=4ac﹣4an=4a(c﹣n),所以③正确;
∵抛物线与直线y=n有一个公共点,
∴抛物线与直线y=n﹣1有2个公共点,
∴一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根,所以④正确.
故答案为:C.
依据抛物线的对称性可知抛物线与x轴的另一个交点在点(-2,0)和(-1,0)之间,则当x=-1时,y>0,于是可对①进行判断;由抛物线的对称轴公式可知可得到b=-2a,于是可对②进行判断;依据抛物线的顶点坐标公式可得到![]() =n,则可对③进行判断;格局抛物线与直线y=n有一个公共点,可得到抛物线与直线y=n-1有2个公共点,于是可对④进行判断.
=n,则可对③进行判断;格局抛物线与直线y=n有一个公共点,可得到抛物线与直线y=n-1有2个公共点,于是可对④进行判断.

 名师点睛字词句段篇系列答案
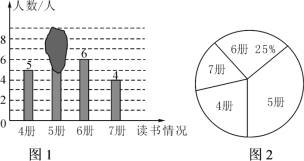
名师点睛字词句段篇系列答案【题目】甲、乙两名工人同时加工同一种零件,现根据两人7天产品中每天出现的次品数情况绘制成如下不完整的统计图和表,依据图、表信息,解答下列问题:
相关统计量表:
量数 人 | 众数 | 中位数 | 平均数 | 方差 |
甲 |
|
| 2 |
|
乙 | 1 | 1 | 1 |
|
次品数量统计表:
天数 人 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
甲 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
乙 | 1 | 0 | 2 | 1 | 1 | 0 |
|
(1)补全图、表.
(2)判断谁出现次品的波动小.
(3)估计乙加工该种零件30天出现次品多少件?