Question

【题目】操作体验

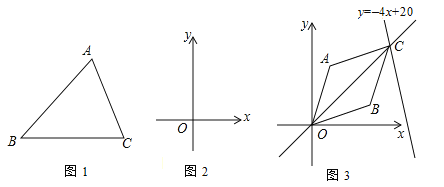
（1）如图1，已知△ABC，请画出△ABC的中线AD，并判断△ABD与△ACD的面积大小关系．

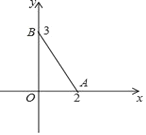
（2）如图2，在平面直角坐标系中，△ABC的边BC在x轴上，已知点A（2，4），B（–1，0），C（3，0），试确定过点A的一条直线l，平分△ABC的面积，请写出直线l的表达式．

综合运用

（3）如图3，在平面直角坐标系中，如果A（1，4），B（3，2），那么在直线y=–4x+20上是否存在一点C，使直线OC恰好平分四边形OACB的面积？若存在，请计算点C的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）S△ABD=S△ACD； （2）y=4x–4； （3）（，）

【解析】

（1）如图1，过A作于点，

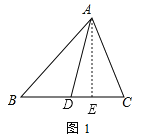
∵AD为边上的中线，

∴

即

（2）如图2，设BC的中点为F，

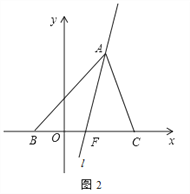
∵直线平分的面积，∴由（1）可知直线过点F，

设直线的表达式为

把A、F的坐标代入可得 ，解得，

∴直线的表达式为

（3）如图3，连接AB交OC于点G，

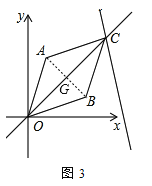
∵直线OC恰好平分四边形OACB的面积，

∴直线OC过AB的中点，即G为AB的中点，

设直线OC的表达式为 则 ，解得a=，∴直线OC表达式为，联立两直线解析式可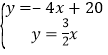得，解得，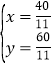

∴存在满足条件的点C，其坐标为（，）．