Question

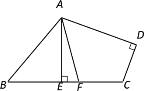
【题目】小明想知道一堵墙上点A的高度（AO⊥OD），但又没有直接测量的工具，于是设计了下面的方案，请你先补全方案，再说明理由．

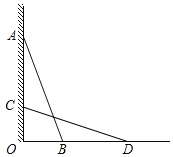
第一步：找一根长度大于OA的直杆，使直杆靠在墙上，且顶端与点A重合，记下直杆与地面的夹角∠ABO；

第二步：使直杆顶端竖直缓慢下滑，直到∠　 　＝∠　 　．标记此时直杆的底端点D；

第三步：测量　 　的长度，即为点A的高度．

说明理由：

Answer 1

【答案】OCD，ABO；OD；理由见解析

【解析】

根据全等三角形的判定和性质定理即可得到结论．

解：第一步：找一根长度大于OA的直杆，使直杆靠在墙上，且顶端与点A重合，记下直杆与地面的夹角∠ABO；

第二步：使直杆顶端竖直缓慢下滑，直到∠OCD＝∠ABO．标记此时直杆的底端点D；

第三步：测量OD的长度，即为点A的高度．

理由：在△AOB与△DOC中，，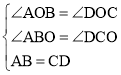

∴△AOB≌△DOC（AAS），

∴OA＝OD．

故答案为：OCD，ABO，OD．