Question

【题目】在平面直角坐标系中，点A（﹣5，0），以OA为直径在第二象限内作半圆C，点B是该半圆周上一动点，连接OB、AB，作点A关于点B的对称点D，过点D作x轴垂线，分别交直线OB、x轴于点E、F，点F为垂足，当DF=4时，线段EF=_______．

Answer 1

【答案】

【解析】试题解析：连结OD，

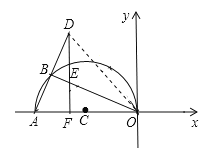
∵点A、点D关于B点对称，

∴OD=OA=5．

在Rt△ODF中，OD=5，DF=4，∠DFO=90°，

∴OF=，

∴AF=OA-OF=2．

∵AO为⊙C的直径，

∴∠ABO=90°，

∴∠DBE=90°=∠DFA，

又∵∠BDE=∠FDA，

∴△BDE∽△FDA，

∴．

在Rt△ADF中，AF=2，DF=4，∠AFD=90°，

∴AD= =2．

∵OA=OD，且OB⊥AD，

∴AB=DB=AD=，

∴DE=，

∴EF=DF-DE=