题目内容
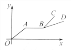
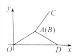
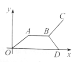
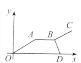
【题目】如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
①abc<0;②a(b+c)>0;③a﹣c=b;④![]() .
.
![]()
其中正确的个数有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】
根据图示,可得c<a<0,b>0,|a|+|b|=|c|,据此逐项判定即可.
∵c<a<0,b>0,
∴abc>0,
∴选项①不符合题意.
∵c<a<0,b>0,|a|+|b|=|c|,
∴b+c<0,
∴a(b+c)>0,
∴选项②符合题意.
∵c<a<0,b>0,|a|+|b|=|c|,
∴-a+b=-c,
∴a-c=b,
∴选项③符合题意.
∵![]() =-1+1-1=-1,
=-1+1-1=-1,
∴选项④不符合题意,
∴正确的个数有2个:②、③.
故选:B.

练习册系列答案
相关题目
【题目】表为小洁打算在某电信公司购买一支MAT手机与搭配一个门号的两种方案.此公司每个月收取通话费与月租费的方式如下:若通话费超过月租费,只收通话费;若通话费不超过月租费,只收月租费.若小洁每个月的通话费均为x元,x为400到600之间的整数,则在不考虑其他费用并使用两年的情况下,x至少为多少才会使得选择乙方案的总花费比甲方案便宜?( )
甲方案 | 乙方案 | |
门号的月租费(元) | 400 | 600 |
MAT手机价格(元) | 15000 | 13000 |
注意事项:以上方案两年内不可变更月租费 | ||
A.500
B.516
C.517
D.600