��Ŀ����
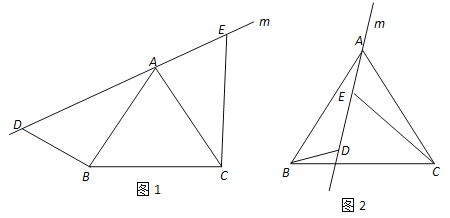
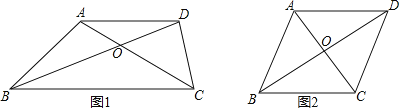
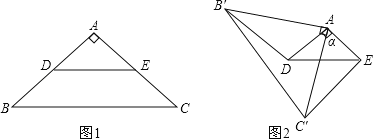
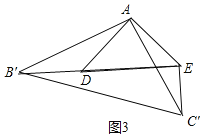
����Ŀ����ͼ1������ABC�У�AB��AC����BAC��90����D��E�ֱ���AB��AC�ߵ��е㣮����ABC�Ƶ�A˳ʱ����תa�ǣ�0����a��180�������õ���AB��C������ͼ2��������DB'��EC'��
��1��̽��DB'��EC'��������ϵ�������ͼ2����֤����
��2����գ�
�ٵ���ת�����Ķ���Ϊ_____ʱ����DB'��AE��
������ת�����У�����B'��D��E��һ��ֱ���ϣ���AD��![]() ʱ����ʱEC���ij�Ϊ_____��
ʱ����ʱEC���ij�Ϊ_____��
���𰸡���1��DB'��EC'��֤�������������2����60������![]() -1��
-1��
��������
��1������ת�����ʿɵá�DAE����B'AC'��90����AB'��AC'��������SAS����֤����ADB'�ա�AEC'���ɵ�DB'��EC'����2����ƽ���ߵ����ʺ�ֱ�������ε����ʿ���⣻��3����ȫ�������ε����ʿɵá�ADB'����AEC'��B'D��C'E���ɵ���ֱ�������ε����ʿɵ�B'C'��![]() AB'��4��DE��
AB'��4��DE��![]() AD��2���ɹ��ɶ�������EC'�ij���
AD��2���ɹ��ɶ�������EC'�ij���
��1��DB'��EC'��
�������£���AB��AC��D��E�ֱ���AB��AC�ߵ��е㣬
��AD��AE��
����ת�ɵã���DAE����B'AC'��90����AB'��AC'��
���DAB'����EAC'����AB'��AC'��AD��AE
���ADB'�ա�AEC'��SAS����
��DB����EC����
��2���١�DB����AE��
���B'DA����DAE��90����
��AD��![]() AB��AB=AB'��
AB��AB=AB'��
��AD��![]() AB'��
AB'��
���AB'D��30����
���DAB'��60����
����ת������60����
�ʴ�Ϊ60����
����ͼ������B'��D��E��һ��ֱ���ϣ�
��AD��![]() ��
��
��AB'��2![]() ��
��
�ߡ�ADE����AB'C'�ǵ���ֱ�������Σ�
��B'C'��![]() AB'��4��DE��
AB'��4��DE��![]() AD��2��
AD��2��
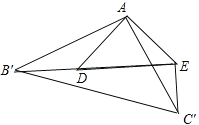
�ɣ�1����֪����ADB'�ա�AEC'��
���ADB'����AEC'��B'D��C'E��
�ߡ�ADB'����DAE+��AED����AEC'����AED+��DEC'��
���DEC'����DAE��90����
��B'C'2��B'E2+C'E2��
��16����2+EC'��2+C'E2��
��CE��![]() ��1��
��1��
�ʴ�Ϊ��![]() ��1��
��1��

 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д� ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�