题目内容
【题目】若一个三角形一条边的平方等于另两条边的乘积,我们称这个三角形是比例三角形.
(1)已知△ABC是比例三角形,AB=1,BC=2,求AC的长.
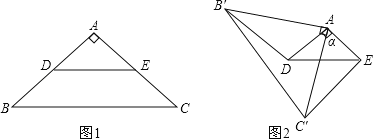
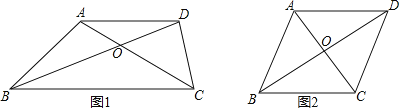
(2)如图1,在四边形ABCD中,AB=AD,对角线BD平分∠ABC,∠BAC=∠ADC
①求证:△ABC是比例三角形
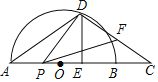
②若AB∥DC,如图2,求![]() 的值.
的值.
【答案】(1)AC=![]() ;(2)①详见解析;②
;(2)①详见解析;②![]() .
.
【解析】
(1)根据比例三角形的定义,分AB2=BCAC、BC2=ABAC、AC2=ABBC三种情况分别代入计算可得;
(2)①先证△ADC∽△CAB,得ADBC=AC2,再由∠ABD=∠CBD,∠ADB=∠DBC,推出AB=AD即可得;②首先证明四边形ABCD是菱形,根据∠BAC=∠ADC可得△ABC是等边三角形,然后根据含30° 直角三角形的性质可得答案.
解:(1)设AC=m.
由题意m2=1×2或12=2m或22=m,
∴m=![]() ,m=
,m=![]() (不符合三角形三边关系定理,舍去),m=4(不符合三角形三边关系定理,舍去),
(不符合三角形三边关系定理,舍去),m=4(不符合三角形三边关系定理,舍去),
故AC=![]() ;
;
(2)①∵AB=AD,
∴∠ABD=∠ADB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠DBC,
∴AD∥BC,
∴∠ACB=∠DAC,
∵∠BAC=∠ADC,
∴△ADC∽△CAB,
∴![]() ,
,
∴ADBC=AC2,
∵∠ABD=∠CBD,∠ADB=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD,
∴ABBC=AC2,
∴△ABC是比例三角形;
②由①知AD∥BC,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AB=AD,
∴四边形ABCD是菱形,
∵∠BAC=∠ADC,且∠BAC=∠BCA,
∴∠ADC=∠BCA,
∴∠ABC=∠BCA=∠BAC,
∴△ABC是等边三角形,
∴BO=![]() AO,DO=
AO,DO=![]() OC,
OC,
∴BO+DO=![]() (OA+OC),
(OA+OC),
∴BD=![]() AC,
AC,
∴![]() =
=![]() .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案