题目内容
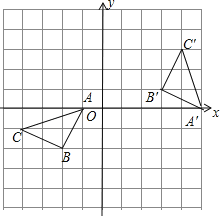
【题目】如图所示,在正方形网格中,△ABC的顶点坐标分别为(﹣1,0),(﹣2,﹣2),(﹣4,﹣1).请在所给直角坐标系中按要求画图和解答下列问题:
(1)将△ABC绕着某点按顺时针方向旋转得到△A′B'C',请直接写出旋转中心的坐标和旋转角度.
(2)画出△ABC关于点A成中心对称的△AED,若△ABC内有一点P(a,b),请直接写出经过这次变换后点P的对称点坐标.
【答案】(1)旋转中心坐标为(2,﹣3),旋转角为90°;(2)作图见解析,(﹣a﹣2,﹣b).
【解析】
(1)作线段BB′,线段AA′的垂直平分线交于点K,点K即为所求.连接AK、A′K,可得∠AKA′=90°,即可得旋转角度数;(2)分别作出C,B的对应点E,D即可,利用中点坐标公式求出对称点的坐标即可.
(1)如图,作线段BB′,线段AA′的垂直平分线交于点K,点K即为所求.
∴旋转中心坐标为K(2,﹣3),
连接AK、A′K,
由网格的特点可知:∠AKA′=90°,
∴旋转角为90°.
(2)如图,△ADE即为所求,
设点P关于点A的对称点为P′(x,y),
∵A(-1,0),P(a,b),点A为PP′的中点,
∴![]() ,
,![]() ,
,
解得:x=-2-a,y=-b,
∴点P(a,b)经过这次变换后点P的对称点坐标为(﹣a﹣2,﹣b).


练习册系列答案
相关题目