题目内容
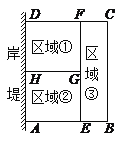
【题目】为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域，而且这三块矩形区域的面积相等．设BC的长度为xm，矩形区域ABCD的面积为ym2．
（1）求AE的长（用x的代数式表示）
（2）当y=108m2时，求x的值
【答案】（1）20-
x（2）4m或36m
【解析】
试题（1）设AE=a，由矩形区域①②的面积和=矩形区域③的面积的2倍．提出BE=a，AB=
a，然后根据周长为80米得出a与x的关系式；．（2）求出y与x之间的函数关系式，令y=108，解方程可得x的值．
试题解析：解：（1）设AE=a，由题意，得AE·AD=2BE·BC,AD=BC,∴BE=a,
AB=a,由题意，得2x+3a+2·a="80," ∴a=20-x ，AE=20-x
（2）y=AB·BC=a·X=（20-x）x,即y=--
+30x（0＜x＜40）
-+30x=108 解得 x1=4,x2=36， 答：x为4m或36m
练习册系列答案
相关题目
