题目内容
【题目】如图(1),A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC,若AB=CD,试证明BD平分EF,若将△DEC的边EC沿AC方向移动变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.

【答案】(1)证明见试题解析;(2)成立.
【解析】
试题分析:(1)先利用HL判定Rt△ABF≌Rt△CDE,得出BF=DE;再利用AAS判定△BFG≌△DEG,从而得出FG=EG,即BD平分EF;
(2)结论仍然成立,同样可以证明得到.
试题解析:(1)证明:∵DE⊥AC,BF⊥AC,∴∠DEG=∠BFE=90°,∵AE=CF,AE+EF=CF+EF,即AF=CE.在Rt△ABF和Rt△CDE中,∵AB=CD,AF=CE,∴Rt△ABF≌Rt△CDE(HL),∴BF=DE.在△BFG和△DEG中,∵∠BFG=∠DEG,∠BGF=∠DGE,BF=DE,∴△BFG≌△DEG(AAS),∴FG=EG,即BD平分EF;
(2)FG=EG,即BD平分EF的结论依然成立.
理由:如图2,连接BE、FD.∵AE=CF,FE=EF,∴AF=CE,∵DE垂直于AC,BF垂直于AC,∴∠AFB=∠CED,BF∥DE,∴在Rt△ABF和Rt△CDE中,∵AF=CE,AB=CD,∴△ABF≌△CDE(HL),∴BF=DE,∴四边形BEDF是平行四边形,∴GE=GF,即:BD平分EF,即结论依然成立.


 阅读快车系列答案
阅读快车系列答案【题目】某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年月平均用水量(单位:吨),并将调查数据进行如下整理:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
频数分布表
分组 | 划记 | 频数 |
2.0<x≤3.5 | 正正 | 11 |
3.5<x≤5.0 |
| 19 |
5.0<x≤6.5 | ||
6.5<x≤8.0 | ||
8.0<x≤9.5 |
| 2 |
合计 | 50 |
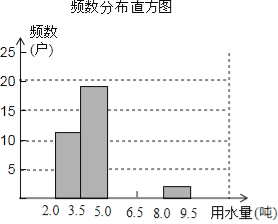
(1)把上面频数分布表和频数分布直方图补充完整;
(2)从直方图中你能得到什么信息?(写出两条即可);
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?





