Question

【题目】如图，△ABC中，AB=5，BC=3，AC=4，以点C为圆心的圆与AB相切，则⊙C的半径为（ ）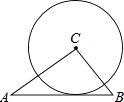

A.2.3
B.2.4
C.2.5
D.2.6

Answer 1

【答案】B
【解析】解：在△ABC中，
∵AB=5，BC=3，AC=4，
∴AC2+BC2=32+42=52=AB2 ，
∴∠C=90°，
如图：设切点为D，连接CD，
∵AB是⊙C的切线，
∴CD⊥AB，
∵S△ABC= ACBC= ABCD，
∴ACBC=ABCD，
即CD= = = ，
∴⊙C的半径为 ，
故选B．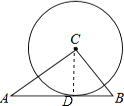

【考点精析】关于本题考查的切线的性质定理，需要了解切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案．