题目内容
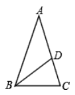
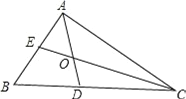
【题目】如图,在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于点O,
(1)求∠AOC的度数;
(2)求证:OE=OD;
(3).猜测AE,CD,AC三者的数量关系,并证明.
【答案】(1)见解析(2)见解析(3)AE+CD=AC.
【解析】
(1)根据△ABC中,∠B=60°,所以∠BAC+∠BCA=120°.因为AD平分∠BAC,CE平分∠ACB,可求出∠AOC=120°;
(2)求出∠AOE=60度.在AC上截取AF=AE,连接OF,易证△AOE≌△AOF,得OE=OF,∠AOE=∠AOF=60°,可证△COD≌△COF,得OD=OF,即可得证;
(3)根据全等得出AE=AF,CD=CF,所以AC=AF+CF=AE+CD,即AE+CD=AC.
(1)在△ABC中,∠B=60°,
∴∠BAC+∠BCA=180°∠B=180°60°=120°.
∵AD平分∠BAC,CE平分∠ACB,
∴∠OAC=∠OAB=![]() ∠BAC,∠OCD=∠OCA=
∠BAC,∠OCD=∠OCA=![]() ∠ACB,
∠ACB,
在△OAC中,∠AOC=180°(∠OAC+∠OCA)
=180°![]() (∠BAC+∠ACB)=180°
(∠BAC+∠ACB)=180°![]() ×120°=120°;
×120°=120°;
(2)∵∠AOC=120°,
∴∠AOE=∠DOC=180°∠AOC=180°120°=60°,
在AC上截取AF=AE,连接OF,如图,
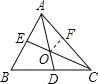
在△AOE和△AOF中,
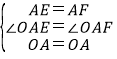
∴△AOE≌△AOF(SAS),
∴OE=OF,
∴∠AOE=∠AOF,
∴∠AOF=60°,
∴∠COF=∠AOC∠AOF=120°60°=60°,
又∠COD=60°,
∴∠COD=∠COF,
在△COD和△COF中,
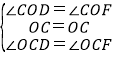 ,
,
∴△COD≌△COF(ASA),
∴OD=OF,
∴OE=OD;
(3)∵△AOE≌△AOF,△COD≌△COF,
∴AE=AF,CF=CD,
又∵AF=AE,
∴AC=AF+CF=AE+CD,
即AE+CD=AC.

 阅读快车系列答案
阅读快车系列答案