Question

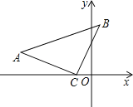
【题目】如图，在△ACB中，∠ACB=90°，AC=BC，C点坐标为（﹣3，0），A点坐标为（﹣8，4），则B点的坐标是_____．

Answer 1

【答案】（1，5）

【解析】

过A和B分别作AD⊥OC于D，BE⊥OC于E，利用已知条件可证明△ADC≌△CEB，再有全等三角形的性质和已知数据即可求出B点的坐标．

过A和B分别作AD⊥OC于D，BE⊥OC于E，
∵∠ACB=90°，
∴∠ACD+∠CAD=90°∠ACD+∠BCE=90°，
∴∠CAD=∠BCE，
在△ADC和△CEB中，

∴△ADC≌△CEB（AAS），
∴DC=BE，AD=CE，
∵点C的坐标为（-3，0），点A的坐标为（-8，4），
∴OC=3，AD=CE=4，BE=CD=8-3=5，
∴则B点的坐标是（1，5），
故答案为：（1，5）．