题目内容
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,对角线
,对角线![]() ,
,![]() 相交于
相交于![]() 点,将直线
点,将直线![]() 绕点
绕点![]() 顺时针旋转,分别交
顺时针旋转,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,下列说法不正确的是( )
,下列说法不正确的是( )

A. 当![]() 时,四边形
时,四边形![]() 一定为平行四边形
一定为平行四边形
B. 当四边形![]() 为直角梯形时,线段
为直角梯形时,线段![]()
C. 当![]() 时,四边形
时,四边形![]() 一定为菱形
一定为菱形
D. 在旋转的过程中,线段![]() 与
与![]() 总相等
总相等
【答案】B
【解析】
根据平行四边形的判定得出AB∥EF,AD∥BC,即可得出四边形ABEF一定为平行四边形;利用直角三角形的面积求出AB×AC=AM×BC,求出EF即可;当∠AOF=45°时,
可得到△BAO是等腰直角三角形,从而得到EF⊥BD.再由OF=OE,根据对角线互相垂直平分的四边形是菱形知,四边形BEDF一定为菱形;通过证明△AEO≌△CEO,可得到AF=EC.
A.当∠AOF=90°时.
∵ABCD中,AB⊥AC,∴AB∥EF.
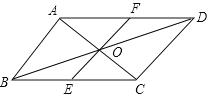
∵AD∥BC,∴四边形ABEF一定为平行四边形.故选项A正确;
B.作AM⊥BC,当四边形ABEF为直角梯形时,∴EF⊥BC,∴AM=EF.
∵AB⊥AC,AB=1,BC=![]() ,∴AC=2,∴AB×AC=AM×BC,∴1×2=AM×
,∴AC=2,∴AB×AC=AM×BC,∴1×2=AM×![]() ,∴AM=
,∴AM=![]() .
.
故选项B错误.
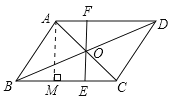
C.当∠AOF=45°时.
∵AB⊥AC,AB=1,BC=![]() ,∴AC=
,∴AC=![]() =2.
=2.
∵OA=OC=![]() AC=1,∴△BAO是等腰直角三角形,∴∠AOB=45°.
AC=1,∴△BAO是等腰直角三角形,∴∠AOB=45°.
∵∠AOF=45°,∴∠BOF=90°,∴EF⊥BD.
∵△AOF≌△CEO,∴OF=OE,根据对角线互相垂直平分的四边形是菱形知,四边形BEDF一定为菱形,故C正确;
D.∵AF∥BE,∴∠FAO=∠OCE.
∵AO=CO,∠AOF=∠COE,∴△AEO≌△CEO,∴AF=EC,故D正确.
故选B.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目







