题目内容
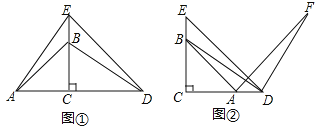
【题目】如图，三角形ABC是边长为6的等边三角形，P是AC边上任意一点（与A、C两点不重合）．Q是CB延长线上一点，且始终满足条件BQ=AP，过P作PE⊥AB于E，连接PQ交AB于D．
（1）如图（1）当∠CQP=30°时．求AP的长．
（2）如图（2），当P在任意位置时，求证：DE=
AB．
【答案】（1）2；（2）证明见解析．
【解析】
试题分析：（1）作PF∥BC交AB于点F．根据等边三角形的性质及直角三角形的性质就可以求出∠QPC=∠DPA=90°，得出AB=3AP而求出结论；
（2）作PF∥BC交AB于点F．根据等边三角形的性质就可以得出△PFD≌△QBD就有DF=DB，由等腰三角形的性质就可以得出AE=EF，由EF+FD=ED就可以得出结论．
试题解析：（1）如图（1），作PF∥BC交AB于点F，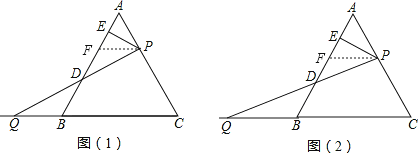
∴∠AFP=∠ABC，∠APF=∠C．∠PFD=∠QBD，∠FPD=∠BQD．
∵△ABC是等边三角形，
∴∠A=∠ABC=∠C=60°．AB=BC=AC．
∴∠AFP=60°，∠APF=60°，
∴∠AFP=∠APF=∠A=60°，
∴△AFP是等边三角形，
∴AF=AP=PF．
∵PE⊥AB，
∴AE=EF．
∵∠CQP=30°，∠C=60°，
∴∠QPC=90°，
∴∠DPA=90°，
∴∠ADP=30°．
∴AD=2AP．
∴AD=2AF．
∵DF+AF=AD，
∴DF+AF=2AF，
∴DF=AF，
∵BQ=AP，
∴BQ=FP．
在△PFD和△QBD中
，
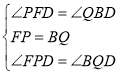∴△PFD≌△QBD（ASA），
∴FD=BD．
∴BD=DF=AF=
AB．
∵AB=6，
∴AF=2，
∴AP=2．
答：AP的长为2；
（2）如图2，作PF∥BC交AB于点F．
∴∠AFP=∠ABC，∠APF=∠C．∠PFD=∠QBD，∠FPD=∠BQD．
∵△ABC是等边三角形，
∴∠A=∠ABC=∠C=60°．AB=BC=AC．
∴∠AFP=60°，∠APF=60°，
∴∠AFP=∠APF=∠C=60°，
∴△AFP是等边三角形，
∴AF=AP=PF．
∵PE⊥AB，
∴AE=EF=
AF．
∵BQ=AP，
∴BQ=FP．
由（1）知，△PFD≌△QBD（ASA），
∴FD=BD=BF．
∵ED=EF+DF=AF+BF，
∴ED=（AF+BF），
∴ED=AB．
