题目内容
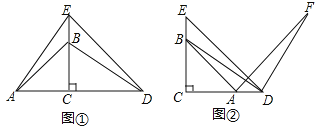
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,且满足
,且满足![]() .
.

(1)![]() 于
于![]() ,交
,交![]() 轴于
轴于![]() ,求
,求![]() 点坐标;
点坐标;
(2)过点![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(3)![]() 为第一象限一点,
为第一象限一点,![]() 交
交![]() 轴于
轴于![]() .在
.在![]() 上截取
上截取![]() ,
,![]() 为
为![]() 的中点,求
的中点,求![]() 的度数.
的度数.
【答案】(1)M(0,2);(2)AN=4;(3)∠OPF=45°.
【解析】
(1)先由条件推出△AOC是等腰直角三角形,再推出△BOM是等腰直角三角形,根据OB=2,得出OM=2,即可得出M的坐标;
(2)由等角的余角相等可得∠BCO=∠OAN=30°,再判定△BOC≌△NOA(ASA),得到BC=NA,再根据Rt△BOC中,BC=2BO=4,即可得AN=4;
(3)连接OF,把△OCF绕点O顺时针旋转90°至△OAD处,连接DP,由旋转可得,AD=CF=EF,∠OCF=∠OAD,OF=OD,再判定△PEF≌△PAD,得出PF=PD,∠FPE=∠DPA,进而判定△OPF≌△OPD,即可出结果.
(1)由题可得,ac≥0,ca≥0,
∴a=c,即OA=OC,
∴△AOC是等腰直角三角形,
∴∠OAD=45,
又∵BD⊥AC,
∴∠ABD=45,
又∵∠BOM=90,
∴△BOM是等腰直角三角形,
∴OB=OM,
∵![]() ,且a=c,
,且a=c,
∴b=2,即OB=2,
∴OM=2,
∴M(0,2);
(2)∵∠CAN=15°,∠OAC=45°,
∴∠OAN=30°,
∵AG⊥BC,CO⊥AO,
∴∠CNG+∠BCO=90°,∠ANO+∠OAN=90°,
∵∠ANO=∠CNG,
∴∠BCO=∠OAN=30°,
在△BOC和△NOA中,
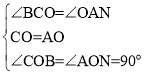
∴△BOC≌△NOA(ASA),
∴BC=NA,
又∵Rt△BOC中,∠BCO=30°,
∴BC=2BO=4,
∴AN=4;
(3)如图3,连接OF,把△OCF绕点O顺时针旋转90°至△OAD处,连接DP,
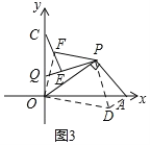
由旋转可得,AD=CF=EF,∠OCF=∠OAD,OF=OD,
∵∠AOQ+∠APQ=180°,
∴∠OAP+∠OQP=180°,
又∵∠EQC+∠OQP=180°,
∴∠OAP=∠EQC,
∴∠PEF=∠PAD,
在△PEF和△PAD中,
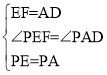
∴△PEF≌△PAD(SAS),
∴PF=PD,∠FPE=∠DPA,
∴∠FPD=∠QPA=90°,
∵在△OPF和△OPD中,
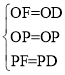
∴△OPF≌△OPD(SSS),
∴∠OPF=∠OPD=![]() ∠FPD=45°.
∠FPD=45°.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案【题目】体育老师为了解本校九年级女生1分钟“仰卧起坐”体育测试项目的达标情况,从该校九年级136名女生中,随机抽取了20名女生,进行了1分钟仰卧起坐测试,获得数据如下:
收集数据:抽取20名女生的1分钟仰卧起坐测试成绩(个)如下:
38 46 42 52 55 43 59 46 25 38
35 45 51 48 57 49 47 53 58 49
(1)整理、描述数据:请你按如下分组整理、描述样本数据,把下列表格补充完整:
范围 | 25≤x≤29 | 30≤x≤34 | 35≤x≤39 | 40≤x≤44 | 45≤x≤49 | 50≤x≤54 | 55≤x≤59 |
人数 |
|
|
|
|
|
|
|
(说明:每分钟仰卧起坐个数达到49个及以上时在中考体育测试中可以得到满分)
(2)分析数据:样本数据的平均数、中位数、满分率如下表所示:
平均数 | 中位数 | 满分率 |
46.8 | 47.5 | 45% |
得出结论:①估计该校九年级女生在中考体育测试中1分钟“仰卧起坐”项目可以得到满分的人数为 ;
②该中心所在区县的九年级女生的1分钟“仰卧起坐”总体测试成绩如下:
平均数 | 中位数 | 满分率 |
45.3 | 49 | 51.2% |
请你结合该校样本测试成绩和该区县总体测试成绩,为该校九年级女生的1分钟“仰卧起坐”达标情况做一下评估,并提出相应建议.