题目内容
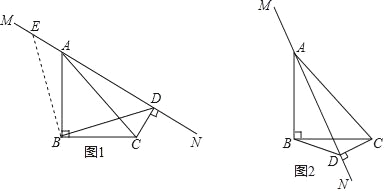
【题目】如图①，点D是等边△ABC的边BC上一点，连接AD，以AD为一边，向右作等边三角形ADE，连接CE，求证：AC=CD+CE.
（类比探究）
(1)如果点D在BC的延长线上，其它条件不变，请在图②的基础上画出满足条件的图形，写出线段AC，CD，CE之间的数量关系，并说明理由.
(2)如果点D在CB的延长线上，请在图③的基础上画出满足条件的图形，并直接写出AC，CD，CE之间的数量关系，不需要说明理由.数量关系：_______.
【答案】证明见解析；类比探究：(1)CE﹣CD=AC；(2)AC=CD﹣CE.
【解析】
先证明△ABD≌△ACE，得出BD=CE，即可证出CE+CD=BD+CD=BC=AC；
类比探究：
（1）先证明△ABD≌△ACE，得出BD=CE，即可证出CE-CD=BD-CD=BC=AC；
（2）先证明△ABD≌△ACE，得出BD=CE，即可得出数量关系：AC=CD-CE．
∵△ABC和△ADE均为等边三角形，
∴AB=AC=BC，AD=AE，∠BAC=∠DAE=60°，
∴∠BAD=∠CAE，
在△ABD和△ACE中，
，
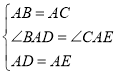∴△ABD≌△ACE(SAS)，
∴BD=CE，
∴CE+CD=BD+CD=BC=AC；
类比探究：（ 1）CE﹣CD=AC；
如图②：
∵△ABC和△ADE均为等边三角形，
∴AB=AC=BC，AD=AE，∠BAC=∠DAE=60°，
∴∠BAD=∠CAE，
在△ABD和△ACE中，
，
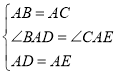∴△ABD≌△ACE(SAS)，
∴BD=CE，
∴CE﹣CD=BD﹣CD=BC=AC.
（ 2）数量关系：AC=CD﹣CE.
如图③：
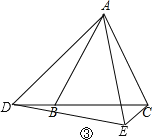
∵△ABC和△ADE均为等边三角形，
∴AB=AC=BC，AD=AE，∠BAC=∠DAE=60°，
∴∠BAD=∠CAE，
在△ABD和△ACE中，
，
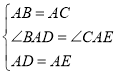∴△ABD≌△ACE(SAS)，
∴BD=CE，
∴CD﹣CE=CD﹣BD=BC=AC.
故答案为：AC=CD﹣CE.
