题目内容
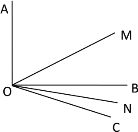
【题目】在△ABC中,AB=AC,∠BAC=120,AD⊥BC,且AD=AB.
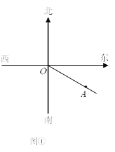
(1)如图1,DE⊥AB,DF⊥AC,垂足分别为点E,F,求证:AE+AF=AD
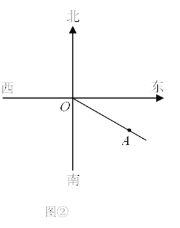
(2)如图2,如果∠EDF=60,且∠EDF两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.


【答案】(1)见解析;![]() ,理由见解析.
,理由见解析.
【解析】
(1)连接BD,证△ABD是等边三角形,得∠ABD=∠BDA=∠DAB=60,再证△BDE≌△ADF(AAS),AF=BE,故AB=AE+BE;
(2)线段AE,AF,AD之间的数量关系为:![]() ,思路如下:
,思路如下:
连接BD,模仿(1)证△BDE≌△ADF(AAS),得![]() ,所以
,所以![]() .
.
∵在△ABC中,AB=AC,AD⊥BC,∠BAC=120
∴∠BAD=∠FAD=60
∵AD=AB
∴△ABD是等边三角形
∴∠ABD=∠BDA=∠DAB=60
∵DE⊥AB,DF⊥AC
∴∠BED=∠DFA=90
在△BDE和△ADF中,
∠BED=∠DFA,∠EBD=∠FAD,BD=DA,
∴△BDE≌△ADF(AAS)
∴AF=BE
∴AB=AE+BE
∴AB=AE+AF
![]() 解:线段AE,AF,AD之间的数量关系为:
解:线段AE,AF,AD之间的数量关系为:![]() ,理由如下:
,理由如下:
连接BD,如图所示:
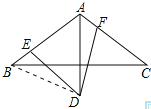
![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 与
与![]() 中,
中,
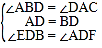 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
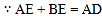 ,
,
![]() .
.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目