题目内容
【题目】对于⊙C与⊙C上的一点A,若平面内的点P满足:射线AP与⊙C交于点Q(点Q可以与点P重合),且![]() ,则点P称为点A关于⊙C的“生长点”.
,则点P称为点A关于⊙C的“生长点”.
已知点O为坐标原点,⊙O的半径为1,点A(-1,0).
(1)若点P是点A关于⊙O的“生长点”,且点P在x轴上,请写出一个符合条件的点P的坐标________;
(2)若点B是点A关于⊙O的“生长点”,且满足![]() ,求点B的纵坐标t的取值范围;
,求点B的纵坐标t的取值范围;
(3)直线![]() 与x轴交于点M,与y轴交于点N,若线段MN上存在点A关于⊙O的“生长点”,直接写出b的取值范围是_____________________________.
与x轴交于点M,与y轴交于点N,若线段MN上存在点A关于⊙O的“生长点”,直接写出b的取值范围是_____________________________.
【答案】(1)(2,0)(答案不唯一);(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】试题分析:
(1)由题意可知,在x轴上找点P是比较简单的,这样的P点不是唯一的,如点(2,0)、(1,0)等;
(2)如图1,在x轴上方作射线AM交⊙O于点M,使tan∠MAO=![]() ,并在射线AM是取点N,使MN=AM,则由题意可知,线段MN上的点都是符合条件的B点,过点M作MH⊥x轴于点H,连接MC,结合已知条件求出点M和点N的纵坐标即可得到所求B点的纵坐标t的取值范围;根据对称性,在x轴的下方得到线段M′N′,同理可求得满足条件的B点的纵坐标t的另一取值范围;
,并在射线AM是取点N,使MN=AM,则由题意可知,线段MN上的点都是符合条件的B点,过点M作MH⊥x轴于点H,连接MC,结合已知条件求出点M和点N的纵坐标即可得到所求B点的纵坐标t的取值范围;根据对称性,在x轴的下方得到线段M′N′,同理可求得满足条件的B点的纵坐标t的另一取值范围;
(3)如图2,3,由![]() 与x轴交于点M,与y轴交于点N,可得点M的坐标为
与x轴交于点M,与y轴交于点N,可得点M的坐标为![]() ,点N的坐标为
,点N的坐标为![]() ,由此结合∠OMN的正切函数可求得∠OMN=60°;
,由此结合∠OMN的正切函数可求得∠OMN=60°;
以点D(1,0)为圆心,2为半径作圆⊙D,则⊙D和⊙O相切于点A,由题意可知,点A关于⊙O的“生长点”都在⊙O到⊙D之间的平面内,包括两个圆(但点A除外).
然后结合题意和∠OMN=60°分b>0和b<0两种情况在图2和图3中求出ON1和ON2的长即可得到b的取值范围了.
试题解析:
(1)由题意可知,在x轴上找点P是比较简单的,这样的P点不是唯一的,如点(2,0)、(1,0)等;
(2)如图1,在x轴上方作射线AM,与⊙O交于M,且使得![]() ,并在AM上取点N,使AM=MN,并由对称性,将MN关于x轴对称,得
,并在AM上取点N,使AM=MN,并由对称性,将MN关于x轴对称,得![]() ,则由题意,线段MN和
,则由题意,线段MN和![]() 上的点是满足条件的点B.
上的点是满足条件的点B.
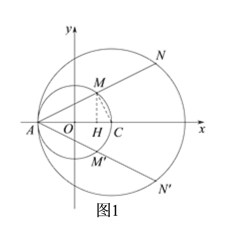
作MH⊥x轴于H,连接MC,
∴ ∠MHA=90°,即∠OAM+∠AMH=90°.
∵ AC是⊙O的直径,
∴ ∠AMC=90°,即∠AMH+∠HMC=90°.
∴ ∠OAM=∠HMC.
∴![]() .
.
∴![]() .
.
设![]() ,则
,则![]() ,
, ![]() ,
,
∴![]() ,解得
,解得![]() ,即点M的纵坐标为
,即点M的纵坐标为![]() .
.
又由![]() ,A为(-1,0),可得点N的纵坐标为
,A为(-1,0),可得点N的纵坐标为![]() ,
,
故在线段MN上,点B的纵坐标t满足: ![]() .
.
由对称性,在线段![]() 上,点B的纵坐标t满足:
上,点B的纵坐标t满足: ![]() .
.
∴ 点B的纵坐标t的取值范围是![]() 或
或![]() .
.
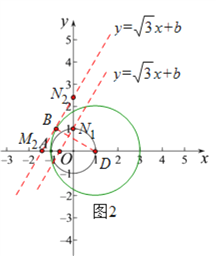
(3)如图2,以点D(1,0)为圆心,2为半径作圆⊙D,则⊙D和⊙O相切于点A,由题意可知,点A关于⊙O的“生长点”都在⊙O到⊙D之间的平面内,包括两个圆(但点A除外).
∵直线![]() 与x轴交于点M,与y轴交于点N,
与x轴交于点M,与y轴交于点N,
∴点M的坐标为![]() ,点N的坐标为
,点N的坐标为![]() ,
,
∴tan∠OMN=![]() ,
,
∴∠OMN=60°,
要在线段MN上找点A关于⊙O的“生长点”,现分“b>0”和“b<0”两种情况讨论:
I、①当直线![]() 过点N1(0,1)时,线段MN上有点A关于⊙O的唯一“生长点”N1,此时b=1;
过点N1(0,1)时,线段MN上有点A关于⊙O的唯一“生长点”N1,此时b=1;
②当直线![]() 与⊙D相切于点B时,线段MN上有点A关于⊙O的唯一“生长点”B,此时直线
与⊙D相切于点B时,线段MN上有点A关于⊙O的唯一“生长点”B,此时直线![]() 与y轴相交于点N2,与x轴相交于点M2,连接DB,则DB=2span>,
与y轴相交于点N2,与x轴相交于点M2,连接DB,则DB=2span>,
∴DM2=![]() ,
,
∴OM2=![]() ,
,
∴ON2=tan60°·OM2=![]() ,此时b=
,此时b=![]() .
.
综合①②可得,当b>0时,若线段MN上存在点A关于⊙O的“生长点”,则b的取值范围为: ![]() ;
;
II、当b<0时,如图3,同理可得若线段MN上存在点A关于⊙O的“生长点”,则b的取值范围为: ![]() ;
;
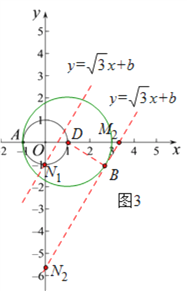
综上所述,若在线段MN上存在点A关于⊙O的“生长点”,则b的取值范围为: ![]() 或
或![]() .
.

【题目】如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数是( )

A. 400 B. 450 C. 500 D. 600
【题目】如图,在△ABC中, ![]() ,
, ![]() °,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至
°,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至![]() ,连接
,连接![]() .已知AB
.已知AB![]() 2cm,设BD为x cm,B
2cm,设BD为x cm,B![]() 为y cm.
为y cm.
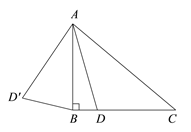
小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整.(说明:解答中所填数值均保留一位小数)
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
| 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 | 0.7 | 0.9 | 1.1 |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:
线段![]() 的长度的最小值约为__________
的长度的最小值约为__________ ![]() ;
;
若![]()
![]() ,则
,则![]() 的长度x的取值范围是_____________.
的长度x的取值范围是_____________.