题目内容
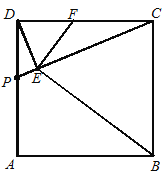
【题目】如图,正方形ABCD中,点P是AD上的一动点(与点D、点A不重合),DE⊥CP,垂足为E,EF⊥BE与DC交于点F.
(1)求证:△DEF∽△CEB;
(2)当点P运动到DA的中点时,求证:点F为DC的中点.
【答案】证明见解析
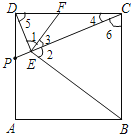
【解析】试题分析:(1)由DE⊥CP,EF⊥BE,则∠1+∠3=∠DEC=90°,∠2+∠3=∠FEB=90°,根据等角的余角相等得∠1=∠2,再根据正方形的性质得∠4+∠6=90°,而∠4+∠5=90°,则∠5=∠6,根据相似三角形的判定即可得到结论;
(2)根据正方形的性质得AD=DC=BC,而点P为DA的中点,则PD=![]() AD=
AD=![]() DC,再根据正切的定义得到tan∠4=
DC,再根据正切的定义得到tan∠4=![]() ,tan∠4=
,tan∠4=![]() ,则
,则![]() ,然后根据△DEF∽△CEB得到
,然后根据△DEF∽△CEB得到![]() ,易得
,易得![]() ,即可得到结论.
,即可得到结论.
试题解析:(1)∵DE⊥CP,EF⊥BE,
∴∠1+∠3=∠DEC=90°,∠2+∠3=∠FEB=90°,
∴∠1=∠2,
∵四边形ABCD是正方形,
∴∠4+∠6=∠DCB=90°,
而在Rt△DEC中,∠4+∠5=90°,
∴∠5=∠6,
∴△DEF∽△CEB;
(2)∵四边形ABCD是正方形,
∴AD=DC=BC,
∵点P为DA的中点,
∴PD=![]() AD=
AD=![]() DC,
DC,
在Rt△PDC中,tan∠4=![]() ,
,
在Rt△DEC中,tan∠4=![]() ,
,
∴![]() ,
,
∵△DEF∽△CEB,
∴![]() ,
,
而CB=DC,
∴![]() ,
,
∴点F为DC的中点.

练习册系列答案
相关题目