题目内容
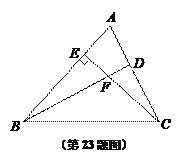
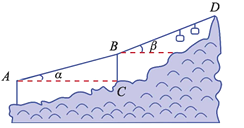
【题目】缆车，不仅提高了景点接待游客的能力，而且解决了登山困难者的难题．如图，当缆车经过点A到达点B时，它走过了700米．由B到达山顶D时，它又走过了700米．已知线路AB与水平线的夹角
为16°，线路BD与水平线的夹角β为20°，点A的海拔是126米．求山顶D的海拔高度（画出设计图，写出解题思路即可）．
【答案】700sin20°+700sin16°+126
【解析】试题分析：本题考查了解直角三角形的实际应用，在Rt△ABC中，根据
可求出BC的长度；在Rt△BDE中，根据
可求出DE的长度；从而可求出D点的海拔高度.
解：如图，
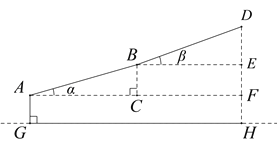
在Rt△ABC中，∠ACB=90°，∠
=16°，AB=700，由sin
，可求BC的长．
即BC=AB·sin
=700sin16°，在Rt△BDE中，∠DBE=90°，∠β=16°，BD=AB=700，由sinβ，可求DE的长．
即DE=BD·sinβ=700sin20°，由矩形性质，可知EF=BC=700sin16°，FH=AG=126．
从而，可求得DH的长．
即DH=DE+EF+FH=700sin20°+700sin16°+126．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
