题目内容
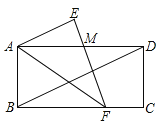
【题目】一天，小明在玩纸片拼图游戏时，发现利用图①中的三种材料各若干，可以拼出一些长方形来解释某些等式，比如图②可以解释为等式：
.
(1)则图③可以解释为等式： .
(2)在虚线框中用图①中的基本图形若干块（每种至少用一次）拼成一个长方形，使拼出的长方形面积为
，并请在图中标出这个长方形的长和宽．
(3)如图④，大正方形的边长为
，小正方形的边长为
，若用
、
表示四个长方形的两边长(
），观察图案，指出以下关系式：(
)
；(
)
；(
)
； (
)
．其中正确的关系式的个数有 个．
【答案】（1）（2a+b）（a+2b）=2a2+5ab+2b2；（2）画图略；（3）4.
【解析】
（1）看图即可得出所求的式子；
（2）画出的矩形边长分别为（2a+b）和（a+3b）即可；
（3）根据图中每个图形的面积之间的关系即可判断出正确的有几个.
解：（1）由分析知：图③所表示的等式为：（2a+b）（a+2b）=2a2+5ab+2b2；
（2）示意图如下
；
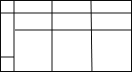（3）（a）观察图形可知正确；
（b）∵4xy=m2-n2，∴xy=
，正确；
（c）∵x+y=m，x-y=n，∴x2-y2=（x+y）（x-y）=mn，∴正确；
（d）x2+y2=（x-y）2+2xy=n2+2×=
，正确；
故正确的有4个，故答案为：4.
考前必练系列答案【题目】如图，在△ABC中， 
， 
°，点D是线段BC上的动点，将线段AD绕点A顺时针旋转50°至
，连接
．已知AB
2cm，设BD为x cm，B
为y cm．
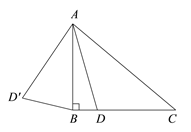
小明根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究，下面是小明的探究过程，请补充完整．（说明：解答中所填数值均保留一位小数）
（1）通过取点、画图、测量，得到了
与
的几组值，如下表：
|
| 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 | 0.7 | 0.9 | 1.1 |
（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象．
（3）结合画出的函数图象，解决问题：
线段
的长度的最小值约为__________ 
；
若
，则
的长度x的取值范围是_____________．
