题目内容
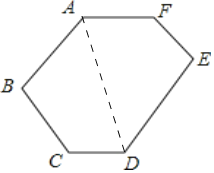
【题目】如图：在六边形ABCDEF中，AF∥CD，AB∥DE，∠BAF=100°，∠BCD=120°.
求∠ABC和∠D的度数．
【答案】∠CDE=100°；∠ABC=140°.
【解析】
连接AD，由AF∥CD得出∠FAD=∠ADC，由AB∥DE得出∠BAD=∠ADE，故可得出∠CDE=∠BAF=100°，∠FAD+∠BAD=∠ADC+∠BAD=100°，再由四边形内角和定理即可得出∠ABC的度数．
解：连接AD
∵AF∥CD，AB∥DE，
∴∠FAD=∠ADC，∠BAD=∠ADE，
∴∠BAF=∠CDE=100°
∵∠ABC+∠DCB+∠BAD+∠ADC=360°，
又∵∠FAB=∠FAD+∠BAD=∠ADC+∠BAD=100°，
∴∠ABC=360°-120°-100°=140°
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
