��Ŀ����
����Ŀ����֪��������ABCD����EAF��45����
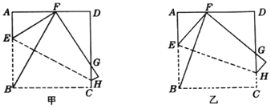
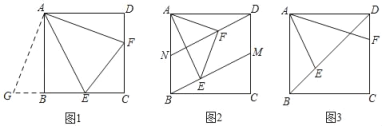
��1����ͼ������E��F�ֱ��ڱ�BC��CD�ϣ�����EF����֤��EF��BE+DF��
ͯ��ͬѧ������˼���ģ��������һ��������½��֤��������ADF�Ƶ�A˳ʱ����ת90��������ABG��������ADF�ա�ABG��
��2����ͼ����M��N�ֱ��ڱ�AB��CD�ϣ���BN��DM������E��F�ֱ���BM��DN�ϣ�����EF��̽�������߶�EF��BE��DF֮�������������ϵ����֤�����Ľ��ۣ�
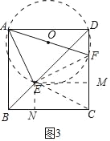
��3����ͼ������E��F�ֱ��ڶԽ���BD����CD�ϣ���FC��2����BE�ij�Ϊ�� ����
���𰸡���1������������2��EF2��BE2+DF2��֤������������3��BE��![]() .
.
��������
��1��������Ŀ����˼·���ɡ�ADF�ա�ABG�Ƴ�AF=AG��DF=BG����DAF=��BAG���õ���EAG=��EAF��ע��Ҫ֤��G��B��E���㹲�ߣ�����֤�á�EAG�ա�EAF����EFת����EG=BG+BE=DF+BE����֤��
��2���ѡ�ADF�Ƶ�A˳ʱ����ת90��á�ABH��֤�����̸���1�����ƣ�֤�á�EAH�ա�EAF����EFת����EH��Ȼ������BN=DM֤���ı���BMDNΪƽ���ı��εá�ABE=��FDM���á�EBH=��ABH+��ABE=��ADF+��MDN=90�㣬��EH2=BE2+BH2��EF2=BE2+DF2��
��3����Ϊ����⣬�ɰѵ�E��F�ƶ�������λ��˼������F��D�غ�ʱ����EΪBD�е㣬��BE=![]() BD����BD=
BD����BD=![]() CD����
CD����![]() CF�����ô�Ϊ
CF�����ô�Ϊ![]() ���ɡ�EAF=��EDF=45�����뵽��A��D��F��E�ĵ㹲Բ����AFΪֱ�������ԡ�AEF=90�㣬��AEFΪ����ֱ�������Σ�����AE=EF=EC������E��EM��CF��M����MΪCF�е㣮���ǵ�BEΪ�����ζԽ����ϵ�һ�Σ�����E��EN��BC�������ֱ�ǡ�BEN����EN=CM����BE=
���ɡ�EAF=��EDF=45�����뵽��A��D��F��E�ĵ㹲Բ����AFΪֱ�������ԡ�AEF=90�㣬��AEFΪ����ֱ�������Σ�����AE=EF=EC������E��EM��CF��M����MΪCF�е㣮���ǵ�BEΪ�����ζԽ����ϵ�һ�Σ�����E��EN��BC�������ֱ�ǡ�BEN����EN=CM����BE=![]() EN=
EN=![]() CM=
CM=![]() ��
��
��1��֤��������ADF�Ƶ�A˳ʱ����ת90�㣬�á�ABG��
���ADF�ա�ABG,
��AF��AG��DF��BG����DAF����BAG.
��������ABCD,
���D����BAD����ABE��90�㣬AB��AD��
���ABG����D��90�㣬��G��B��C��ͬһֱ����.
�ߡ�EAF��45�㣬
���DAF+��BAE��90�㩁45�㣽45�㣬
���EAG����BAG+��BAE����DAF+��BAE��45�㣬
����EAG����EAF.
�ڡ�EAG���EAF�У�
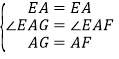 ��
��
���EAG�ա�EAF��SAS����
��EG��EF.
��BE+DF��BE+BG��EG��
��EF��BE+DF��
��2��EF2��BE2+DF2��֤�����£�
����ADF�Ƶ�A˳ʱ����ת90�㣬�á�ABH������ͼ2����
���ADF�ա�ABH��
��AF��AH��DF��BH����DAF����BAH����ADF����ABH��
�ߡ�EAF��45�㣬
���DAF+��BAE��90�㩁45�㣽45�㣬
���EAH����BAH+��BAE����DAF+��BAE��45�㣬
����EAH����EAF��
�ڡ�EAH���EAF�У�
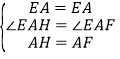 ,
,
���EAH�ա�EAF��SAS��,
��EH��EF.
��BN��DM��BN��DM,
���ı���BMDN��ƽ���ı���,
���ABE����MDN,
���EBH����ABH+��ABE����ADF+��MDN����ADM��90��,
��EH2��BE2+BH2��
��EF2��BE2+DF2��
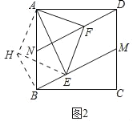
��3������ADF�����Բ��O������EF��EC������E�ֱ���EM��CD��M��EN��BC��N����ͼ3����
�ߡ�ADF��90�㣬
��AFΪ��Oֱ��.
��BDΪ������ABCD�Խ��ߣ�
���EDF����EAF��45�㣬
���E�ڡ�O�ϣ�
���AEF��90�㣬
���AEFΪ����ֱ�������Σ�
��AE��EF.
�ڡ�ABE���CBE�У�
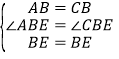
���ABE�ա�CBE��SAS����
��AE��CE��
��CE��EF.
��EM��CF��CF��2��
��CM��![]() CF��1��
CF��1��
��EN��BC����NCM��90�㣬
���ı���CMEN�Ǿ��Σ�
��EN��CM��1��
�ߡ�EBN��45�㣬
��BE��![]() EN��
EN��![]() ��
��
�ʴ�Ϊ��![]() .
.

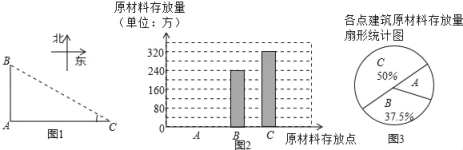
����Ŀ��������н���2017�������Ǩ���山�ո��³ǣ���У���̽������������ݱ�Ľ��У������̲�������Աͬ�⣬��λͬѧǰ�����ؽ������ʵ�������ͼ��A��B��C����������ԭ���ϴ�ŵ㣬��B��C�ֱ�λ�ڵ�A����������������AC��400�ף����˷ֱ��á�C�Ķ��������
�� | �� | �� | �� | |
��C����λ���ȣ� | 34 | 36 | 38 | 40 |
�����ֵ����˸���Ľ������ϴ�������������������в�������ͳ����ͼ����ͼ��
��1������С�C������ƽ����![]() ��
��
��2����A���Ľ���ԭ���ϴ������������ͼ����������
��3���ã�1���е�![]() ��Ϊ��C�Ķ�����Ҫ��A����ȫ������ԭ�����ص�·AB�˵�B������֪��1������ԭ����ÿ�ķ���Ϊ0.1Ԫ��������ȫ������ԭ��������ķ��ã���ע��sin37����0.6��cos37����0.8��tan37����0.75��
��Ϊ��C�Ķ�����Ҫ��A����ȫ������ԭ�����ص�·AB�˵�B������֪��1������ԭ����ÿ�ķ���Ϊ0.1Ԫ��������ȫ������ԭ��������ķ��ã���ע��sin37����0.6��cos37����0.8��tan37����0.75��