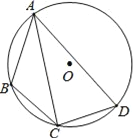
题目内容
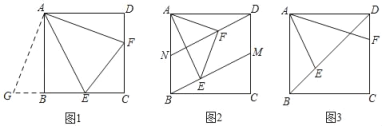
【题目】如图所示,将正方形![]() 折叠,使顶点
折叠,使顶点![]() 与
与![]() 边上的一点
边上的一点![]() 重合(
重合(![]() 不与端点
不与端点![]() ,
,![]() 重合),折痕交
重合),折痕交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,边
,边![]() 折叠后与边
折叠后与边![]() 交于点
交于点![]() ,连接
,连接![]() ,连接
,连接![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)求证:![]() .
.
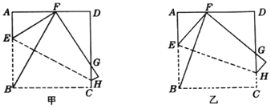
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)由![]() ,可求∠AFB=60°.由折叠的性质求出∠2=30°,从而
,可求∠AFB=60°.由折叠的性质求出∠2=30°,从而![]() ,由30°角的性质可求EF=2AE=20,由此得BE=EF=20,所以AB=30,由锐角的余弦函数求出BF的长;
,由30°角的性质可求EF=2AE=20,由此得BE=EF=20,所以AB=30,由锐角的余弦函数求出BF的长;
(2)如图,过![]() 作
作![]() 于
于![]() 点,连接
点,连接![]() .先根据“AAS”证明
.先根据“AAS”证明![]() ,再根据“HL”证明
,再根据“HL”证明![]() ,然后可证明结论正确.
,然后可证明结论正确.
(1)如图,
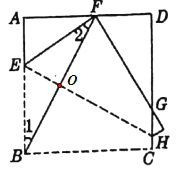
![]() ,
,
∴∠AFB=90°-30°=60°.
∵折叠后![]() 点落在
点落在![]() 点处,
点处,
![]() ,
,![]() ,
,
![]() ,EF=BF,
,EF=BF,
∠AFE=∠AFB-![]()
∴EF=2AE=20,
AB=AE +BE=30,
sin∠AFB=![]()
BF=![]() =
=![]() =
=![]()
(2)如图,过![]() 作
作![]() 于
于![]() 点,连接
点,连接![]() .
.
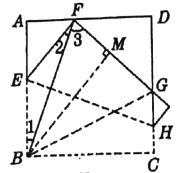
![]() 在正方形
在正方形![]() 中,折叠后
中,折叠后![]() 点落在
点落在![]() 点处,
点处,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
又![]() ,
,
![]() .
.
又![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
又![]() ,
,
![]() .
.
在![]() 与
与![]() 中,
中,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目