题目内容
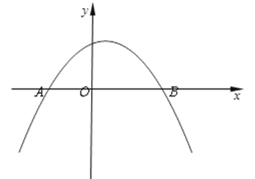
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于点
相交于点![]() 和点
和点![]() 两点.
两点.
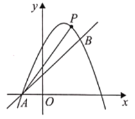
(1)求抛物线的函数表达式;
(2)若点![]() 是位于直线
是位于直线![]() 上方抛物线上的一动点,当
上方抛物线上的一动点,当![]() 的面积
的面积![]() 最大时,求此时
最大时,求此时![]() 的面积
的面积![]() 及点
及点![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 是等腰三角形?若存在,直接写出
是等腰三角形?若存在,直接写出![]() 点的坐标(不用说理);若不存在,请说明理由.
点的坐标(不用说理);若不存在,请说明理由.
【答案】(1)所求抛物线的函数表达式为![]() ;(2)
;(2)![]() 的面积
的面积![]() 有最大值是
有最大值是![]() ,此时点
,此时点![]() 坐标为
坐标为![]() ;(3)存在点
;(3)存在点![]() 坐标为
坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先根据点B在直线y=x+1求出其坐标,再将A,B坐标代入抛物线解析式求解可得;
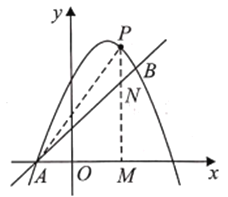
(2)作PM⊥x轴于点M,交AB于点N,设点P的坐标为(m,-m2+2m+3),点N的坐标为(m,m+1),依据S△PAB=S△PAN+S△PBN列出函数解析式,利用二次函数的性质求解可得;
(3)设点Q坐标为(n,0),结合各点坐标得出QA2=(-1-n)2,QB2=(2-n)2+9,AB2=18,再根据等腰三角形的定义分三种情况分别求解可得.
解(1)![]() 点
点![]() 在直线
在直线![]() 上,
上,
![]() ,
,
![]() 点
点![]() 坐标为
坐标为![]() ,
,
![]() 点
点![]() 和点
和点![]() 在抛物线
在抛物线![]() 上,
上,
![]() ,
,
解得![]() ,
,
![]() 所求抛物线的函数表达式为
所求抛物线的函数表达式为![]() ;
;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,
,
设点![]() 的横坐标为
的横坐标为![]() ,
,
则点![]() 的坐标为
的坐标为![]() ,
,
点![]() 的坐标为
的坐标为![]() ,
,
![]() 点
点![]() 是位于直线
是位于直线![]() 上方,
上方,
![]()
![]()
![]() .
.
![]() 的面积
的面积![]()
![]()

![]() ,
,![]()
![]() 抛物线开口向下,又
抛物线开口向下,又![]() ,
,
![]() 当
当![]() 时,
时,
![]() 的面积
的面积![]() 有最大值,
有最大值,
最大值是![]() .
.
此时点![]() 坐标为
坐标为![]() ;
;
(3)存在点![]() 坐标为
坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目