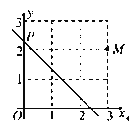题目内容
【题目】如图,在平面直角坐标系中,直线y=-x-3与抛物线y=x2+mx+n相交于A、B两个不同的点,其中点A在x轴上.
(1)n=3m-9(用含m的代数式表示);
(2)若点B为该抛物线的顶点,求m、n的值;
(3)①设m=-2,当-3≤x≤0时,求二次函数y=x2+mx+n的最小值;
②若-3≤x≤0时,二次函数y=x2+mx+n的最小值为-4,求m的值.
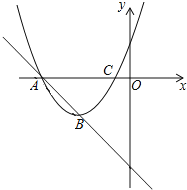
【答案】(1)3m-9;(2)m=4,n=3和m=6,n=9;(3)①n;②m=2.
【解析】
(1)求出点A坐标(-3,0)代入抛物线解析式即可.
(2)利用配方法求出顶点坐标,代入直线解析式即可.
(3)分三种情形①当![]() ≤-3时②当-3<
≤-3时②当-3<![]() ≤0时③当
≤0时③当![]() >0时,分别列出方程即可解决.
>0时,分别列出方程即可解决.
解:(1)∵点A坐标(-3,0)代入抛物线y=x2+mx+n,得9-3m+n=0,
∴n=3m-9.
故答案为3m-9.
(2)∵抛物线为y=x2+mx+3m-9=![]() ,
,
∴顶点为(![]() ),
),
∴![]() ,
,
整理得m2-10m+24=0,
∴m=4或6.
∴m=4,n=3和m=6,n=9.
(3)∵-3≤x≤0时,二次函数y=x2+mx+n的最小值为-4,y=x2+mx+3m-9=![]() +3m-9,
+3m-9,
①当![]() ≤-3时,x=-3时,y=-4,
≤-3时,x=-3时,y=-4,
∴9-3m+3m-9=-4,
无解不合题意.
②当-3<![]() ≤0时,x=时,y=-4,
≤0时,x=时,y=-4,
∴-![]() +3m-9=-4,
+3m-9=-4,
∴m=2或-10(舍弃)
∴m=2.
③当![]() >0时,x=O时,y=-4,
>0时,x=O时,y=-4,
∴3m-9=-4,
∴m=![]() 不合题意舍弃.
不合题意舍弃.
综上所述m=2.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案【题目】用水平线和竖起线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数为a,内部的格点个数为b,则S=![]() a+(b-1).
a+(b-1).
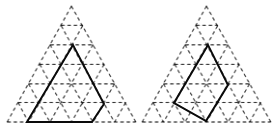
对于正三角形网格中的类似问题也有对应结论:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图是该正三角形格点中的两个多边形(设格点多边形的面积为S,该多边形各边上的格点个数为m,内部的格点个数为n):
(1)根据图中提供的信息填表:
m | n-1 | s | |
多边形1 | 11 | ______ | 15 |
多边形2 | 8 | 1 | ______ |
… | … | … | … |
(2)则S与m、m-1之间的关系为______(用含m、n的代数式表示).