题目内容
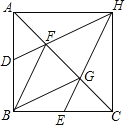
【题目】如图,ABCD的对角线![]() 、
、![]() 交于点
交于点![]() ,顺次联结ABCD各边中点得到的一个新的四边形,如果添加下列四个条件中的一个条件:①
,顺次联结ABCD各边中点得到的一个新的四边形,如果添加下列四个条件中的一个条件:①![]() ⊥
⊥![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,可以使这个新的四边形成为矩形,那么这样的条件个数是()
,可以使这个新的四边形成为矩形,那么这样的条件个数是()

A. 1个;B. 2个;
C. 3个;D. 4个.
【答案】C
【解析】
根据顺次连接四边形的中点,得到的四边形形状和四边形的对角线位置、数量关系有关,利用三角形中位线性质可得:当对角线垂直时,所得新四边形是矩形.逐一对四个条件进行判断.
解:顺次连接四边形的中点,得到的四边形形状和四边形的对角线位置、数量关系有关,利用三角形中位线性质可得:当对角线垂直时,所得新四边形是矩形.
①∵AC⊥BD,∴新的四边形成为矩形,符合条件;
②∵四边形ABCD是平行四边形,∴AO=OC,BO=DO.
∵C△ABO=C△CBO,∴AB=BC.
根据等腰三角形的性质可知BO⊥AC,∴BD⊥AC.所以新的四边形成为矩形,符合条件;
③∵四边形ABCD是平行四边形,∴∠CBO=∠ADO.
∵∠DAO=∠CBO,∴∠ADO=∠DAO.
∴AO=OD.
∴AC=BD,∴四边形ABCD是矩形,连接各边中点得到的新四边形是菱形,不符合条件;
④∵∠DAO=∠BAO,BO=DO,
∴AO⊥BD,即平行四边形ABCD的对角线互相垂直,
∴新四边形是矩形.符合条件.
所以①②④符合条件.
故选:C.

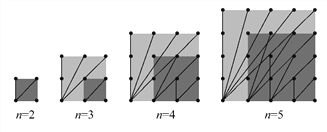
【题目】探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与![]() ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1, ![]() ,2,
,2, ![]() ,2
,2![]() 五种,比n=2时增加了3种,即S=2+3=5.
五种,比n=2时增加了3种,即S=2+3=5.
(1)观察图形,填写下表:
钉子数(n×n) | S值 |
2×2 | 2 |
3×3 | 2+3 |
4×4 | 2+3+(____) |
5×5 | (________) |
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).
(3)对n×n的钉子板,写出用n表示S的代数式.