��Ŀ����
����Ŀ��������н���2017�������Ǩ���山�ո��³ǣ���У���̽������������ݱ�Ľ��У������̲�������Աͬ�⣬��λͬѧǰ�����ؽ������ʵ�������ͼ��A��B��C����������ԭ���ϴ�ŵ㣬��B��C�ֱ�λ�ڵ�A����������������AC��400�ף����˷ֱ��á�C�Ķ��������
�� | �� | �� | �� | |
��C����λ���ȣ� | 34 | 36 | 38 | 40 |
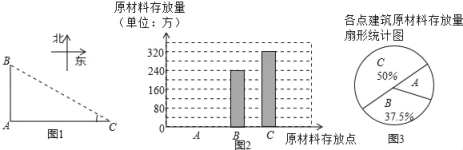
�����ֵ����˸���Ľ������ϴ�������������������в�������ͳ����ͼ����ͼ��
��1������С�C������ƽ����![]() ��
��
��2����A���Ľ���ԭ���ϴ������������ͼ����������
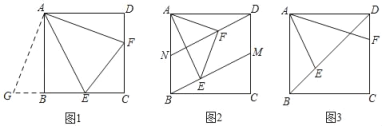
��3���ã�1���е�![]() ��Ϊ��C�Ķ�����Ҫ��A����ȫ������ԭ�����ص�·AB�˵�B������֪��1������ԭ����ÿ�ķ���Ϊ0.1Ԫ��������ȫ������ԭ��������ķ��ã���ע��sin37����0.6��cos37����0.8��tan37����0.75��
��Ϊ��C�Ķ�����Ҫ��A����ȫ������ԭ�����ص�·AB�˵�B������֪��1������ԭ����ÿ�ķ���Ϊ0.1Ԫ��������ȫ������ԭ��������ķ��ã���ע��sin37����0.6��cos37����0.8��tan37����0.75��
���𰸡���1��![]() ��37���ȣ�����2��ԭ���ϵ��ܴ������640������A���Ĵ������80������3������ȫ������ԭ��������ķ�����2400Ԫ��
��37���ȣ�����2��ԭ���ϵ��ܴ������640������A���Ĵ������80������3������ȫ������ԭ��������ķ�����2400Ԫ��
��������
��1������ƽ������ʽ������⣻
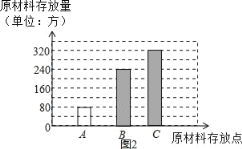
��2������C�ֲ�����320����ռ50%����������ܷ����������ܷ������Զ�Ӧ�İٷֱȼ������A���Ĵ������
��3������A���Ĵ��������AB�ij��ٳ���0.1���ɣ�
��1��![]() ��
��![]() ��34+36+38+40����37���ȣ���
��34+36+38+40����37���ȣ���
��2��ԭ���ϵ��ܴ�����ǣ�320��50%��640��������
����A���Ĵ�����ǣ�640��1��50%��37.5%����80��������
 ��
��
��3������ֱ����ABC�У�tanC��![]() ��
��
��AB��ACtan37����400��0.75��300���ף���
������ȫ������ԭ��������ķ����ǣ�80��300��0.1��2400��Ԫ����

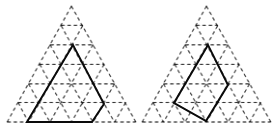
����Ŀ����ˮƽ�ߺ������߽�ƽ��ֳ����ɸ��߳�Ϊ1��С�����θ��ӣ�С�����εĶ����Ϊ��㣬�Ը��Ϊ����Ķ���γ�Ϊ������Σ��������ε����ΪS���ö���θ����ϵĸ�����Ϊa���ڲ��ĸ�����Ϊb����S=![]() a+(b-1)��
a+(b-1)��
�����������������е���������Ҳ�ж�Ӧ���ۣ���������������ÿ��С�����������Ϊ1��С�������εĶ���Ϊ��㣬�Ը��Ϊ����Ķ���γ�Ϊ������Σ���ͼ�Ǹ��������θ���е����������(�������ε����ΪS���ö���θ����ϵĸ�����Ϊm���ڲ��ĸ�����Ϊn)��
(1)����ͼ���ṩ����Ϣ�����
m | n-1 | s | |
�����1 | 11 | ______ | 15 |
�����2 | 8 | 1 | ______ |
�� | �� | �� | �� |
(2)��S��m��m-1֮��Ĺ�ϵΪ______(�ú�m��n�Ĵ���ʽ��ʾ)��