Question

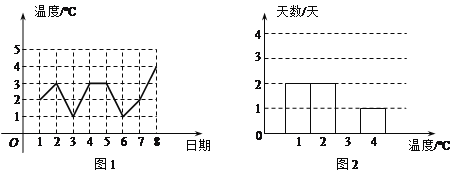
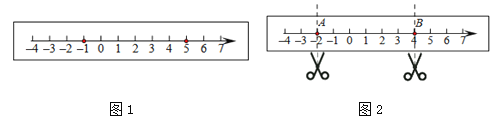
【题目】如图1，在一张长方形纸条上画一条数轴．

(1)折叠纸条使数轴上表示的点与表示5的点重合，折痕与数轴的交点表示的数是 ；

(2)如果数轴上两点之间的距离为8，经过(1)的折叠方式能够重合，那么左边这个点表示的数是 ；

(3)如图2，点A、B表示的数分别是、，数轴上有点C，使得AC=2BC，那么点C表示的数是 ；

(4)如图2，若将此纸条沿A、B两处剪开，将中间的一段纸条对折，使其左右两端重合，这样连续对折次后，再将其展开，求最左端的折痕与数轴的交点表示的数．（用含的代数式表示）

Answer 1

【答案】(1)2；(2)； (3)2或10；(4).

【解析】

（1）找出5表示的点与﹣1表示的点组成线段的中点表示数，然后结合数轴即可求得答案；

（2）由2平分两个点组成的线段，得到左边的点为2－距离的一半，从而可求得答案；

（3）设点C表示的数为x，分三种情况讨论：①点C在A的左侧，②点C在A和B之间，③点C在B的右侧．

（4）先求出每两条相邻折痕的距离，进一步得到最左端的折痕和最右端的折痕与数轴的交点表示的数，即可求得答案．

（1）（﹣1+5）÷2=4÷2=2．

故折痕与数轴的交点表示的数为2；

（2）2－8÷2=2－4=－2；

（3）设点C表示的数为x，分三种情况讨论：

①点C在A的左侧，此时AC＜BC，与AC=2BC矛盾，此种情况不成立；

②点C在A和B之间，此时：x+2=2(4－x)，解得：x=2；

③点C在B的右侧，此时：x+2=2(x－4)，解得：x=10．

综上所述：点C表示的数是2或10．

（4）∵对折n次后，每两条相邻折痕的距离为=，∴最左端的折痕与数轴的交点表示的数是﹣2+．