题目内容
【题目】以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.
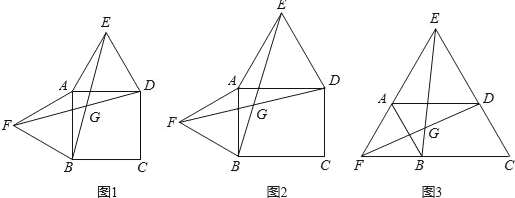
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
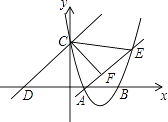
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.
【答案】(1)EB=FD;(2)EB=FD,证明见解析;(3)不变,∠EGD=60°
【解析】试题分析:(1)EB=FD,利用正方形的性质、等边三角形的性质和全等三角形的证明方法可证明△AFD≌△ABE,由全等三角形的性质即可得到EB=FD;
(2)当四边形ABCD为矩形时,EB和FD仍旧相等,证明的思路同(1);
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD不发生变化,是一定值,为60°.
试题解析:
(1)EB=FD,
理由如下:
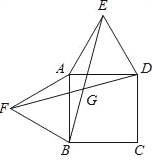
∵四边形ABCD为正方形,
∴AB=AD,
∵以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,
∴AF=AE,∠FAB=∠EAD=60°,
∵∠FAD=∠BAD+∠FAB=90°+60°=150°,
∠BAE=∠BAD+∠EAD=90°+60°=150°,
∴∠FAD=∠BAE,
在△AFD和△ABE中,
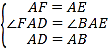 ,
,
∴△AFD≌△ABE,
∴EB=FD;
(2)EB=FD.
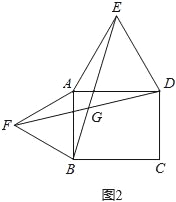
证:∵△AFB为等边三角形
∴AF=AB,∠FAB=60°
∵△ADE为等边三角形,
∴AD=AE,∠EAD=60°
∴∠FAB+∠BAD=∠EAD+∠BAD,
即∠FAD=∠BAE
∴△FAD≌△BAE
∴EB=FD;
(3)解:
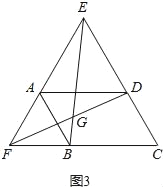
同(2)易证:△FAD≌△BAE,
∴∠AEB=∠ADF,
设∠AEB为x°,则∠ADF也为x°
于是有∠BED为(60﹣x)°,∠EDF为(60+x)°,
∴∠EGD=180°﹣∠BED﹣∠EDF
=180°﹣(60﹣x)°﹣(60+x)°
=60°.