题目内容
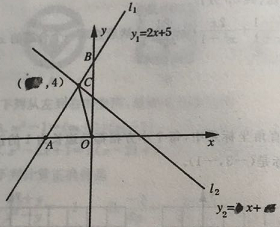
【题目】如图，已知抛物线y=ax2+bx+c（a＜0，c＞0）与x轴交于A，B两点，与y轴交于点C，其对称轴l为x=﹣1，直线y=kx+m经过A，C两点，与抛物线的对称轴l交于点D，且AD=2CD，连接BC，BD．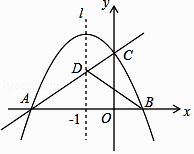
（1）求A，B两点的坐标；
（2）求证：a=﹣k；
（3）若△BCD是直角三角形，求抛物线的解析式．
【答案】
（1）
解：如图，设对称轴l与x轴的交点为E，
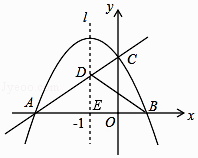
∵l∥y轴，
∴ 
= 
，且AD=2DC，
∴AE=2EO，
∵对称轴l为x=1，
∴E（﹣1，0），则EO=1，
∴AE=2，则OA=3，
∴A（﹣3，0），
∵A、B关于对称轴l对称，
∴BE=AE=2，则OB=1，
∴B（1，0）
（2）
证明：∵抛物线经过A（﹣3，0）和B（1，0），
∴抛物线解析式为y=a（x+3）（x﹣1），即y=ax2+2ax﹣3a，
∵抛物线与y轴交于点C，
∴C（0，﹣3a），
∵直线y=kx+m经过A、C两点，
∴ 
，解得m=3k，
∴C（0，3k），
∴﹣3a=3k，即a=﹣k
（3）
解：由（1）、（2）可知B（1，0），C（0，3k），D（﹣1，2k），
∴BC2=1+9k2，BD2=4+4k2，CD2=1+k2，
∵在Rt△BCO中，∠CBD＜∠CBO＜90°，
∴∠CBD为锐角，
∴只可能当∠BCD或∠BDC为直角时，△BCD才是直角三角形，
①当∠BCD为直角时，则有BC2+CD2=BD2，
∴1+9k2+1+k2=4+4k2，即k2= 
，
∵k＞0，
∴k= 
，
∴a=﹣k=﹣ ，
∴抛物线解析式为y=﹣ x2﹣ 
x+ 
；
②当∠BDC为直角时，则有BD2+CD2=BC2，
∴4+4k2+1+k2=1+9k2，即k2=1，
∵k＞0，
∴k=1，
∴a=﹣k=﹣1，
∴抛物线解析式为y=﹣x2﹣2x+3；
综上可知抛物线解析式为y=﹣ x2﹣ x+ 或y=﹣x2﹣2x+3
【解析】（1）设对称轴x与x轴交点为E，由平行线分线段成比例可求得AE的长，则可求得A点坐标，再利用抛物线的对称性可求得B点坐标；（2）把A、B两点的坐标代入抛物线解析式，可用a表示出C点的坐标，再由直线AC的解析式可用k表示出C点坐标，则可得到a和k的关系；（3）用k可表示出C、D的坐标，利用勾股定理可表示出BC2、BD2和CD2 ， 分∠BDC=90°和∠BCD=90°两种情况可分别求得k的值，可求得k的值，可求得a的值，则可求出抛物线的解析式．
