题目内容
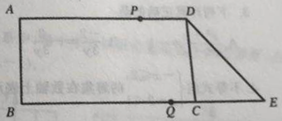
【题目】已知:正方形纸片ABCD的边长为4,将该正方形纸片沿EF折叠(E,F分别在AB,CD边上),使点B落在AD边上的点M处,点C落在点N处,MN与CD交于点P.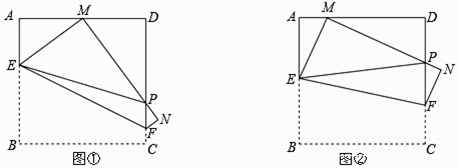
(1)如图①,连接PE,若M是AD边的中点.
①写出图中与△PMD相似的三角形.
②求△PMD的周长.
(2)如图②,随着落点M在AD边上移动(点M不与A、D重合),△PDM的周长是否发生变化?请说明你的理由.
【答案】
(1)
解:①依据翻折的性质可知∠EMP=∠B=90°,∠C=∠N=90°
∴∠AME+∠PMD=90°.
又∵∠AME+∠AEM=90°,
∴∠AEM=∠PMD.
又∵∠A=∠D,
∴△AME∽△DPM.
∵∠MPD=∠FPN,∠D=∠N=90°
∴△MPD∽△FPN.
∵△AME∽△DPM,
∴ ![]() .
.
又∵AM=MD,
∴ ![]() .
.
又∵∠EMP=∠D=90°,
∴△EMP∽△MDP.
所以有:△AME∽△DPM,△AME∽△DPM,△EMP∽△MDP.
②∵四边形ABCD是正方形,
∴AD=AB=4.
∵点M是AD边中点,
∴AM=DM=2.
由折叠的性质得:ME=BE,
∴△MEA的周长为6.
在Rt△MEA中,设AE=x,则ME=4﹣x.
∴x2+22=(4﹣x)2,解得:x= ![]() .
.
∵△PMD∽△MEA,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() .
.
∴△PMD的周长为8
(2)
解:△PMD的周长不变.
设AM=m,AE=n,则DM=4﹣m,EM=4﹣n,△AEM的周长=4+m.
在Rt△AME中,依据勾股定理可知:m2+n2=(4﹣n)2,即8n=16﹣m2.
∵△PMD∽△MEA,
∴ ![]() =
= ![]() .
.
∴△PMD的周长= ![]() =
= ![]() =
= ![]() =8
=8
【解析】(1)①依据两组角对应相等的三角形相似可证明△AEM∽△DMP,△PFN∽△PMD,然后依据两组边对应成比例且夹角相等的两个三角形相似证明△EMP∽△MDP即可;②设AE=x,则EM=4﹣x,在Rt△AEM中,依据勾股定理可求得x的值,然后可求得△AEM的周长,然后依据相似三角形的周长比等于相似比求解即可;(2)设AM=m,AE=n,则DM=4﹣m,EM=4﹣n.在Rt△AEM中,依据勾股定理和完全平方公式可得到8n=16﹣m2 , 然后可△PMD∽△MEA可求得△PMD的周长.
【考点精析】根据题目的已知条件,利用翻折变换(折叠问题)和相似三角形的应用的相关知识可以得到问题的答案,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等;测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.

 阅读快车系列答案
阅读快车系列答案【题目】谷歌人工智能AlphaGo机器人与李世石的围棋挑战赛引起人们的广泛关注,人工智能完胜李世石.某教学网站开设了有关人工智能的课程并策划了A,B两种网上学习的月收费方式:
收费 方式 | 月使用费(元) | 包时上网 时间(h) | 超时费(元/min) |
A | 7 | 25 | 0.6 |
B | 10 | 50 | 0.8 |
设小明每月上网学习人工智能课程的时间为x小时,方案A,B的收费金额分别为yA元,yB元.
(1)当x≥50时,分别求出yA,yB与x之间的函数关系式;
(2)若小明3月份上该网站学习的时间为60小时,则他选择哪种方式上网学习合算?