Question

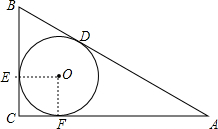
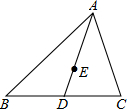
如图，在△ABC中，∠C=90°，∠A和∠B的平分线相交于P点，又PE⊥AB于点E，若BC=2，AC=3，则AE•EB=______．

Answer 1

设Rt△ABC内切圆P的半径为r．
AB=

AC2+BC2

=

32+22

=

13

AE=AM=AC-r=3-r，BE=BN=BC-r=2-r
AB=AE+BE=（3-r）+（2-r）=5-2r
∴

13

=5-2r，即r=

5- 13

2

∴AE•BE=（3-r）•（2-r）=（3-

5- 13

2

）•（2-

5- 13

2

）=

13 +1

2

•

13 -1

2

=

13-1

4

=3
故答案为3．