题目内容
如图，已知在Rt△ABC中，∠C=90°，内切圆的半径为3cm，外接圆的半径为12.5cm，求△ABC的三边长．
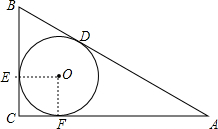
∵在Rt△ABC中，∠C=90°，内切圆的半径为3cm，外接圆的半径为12.5cm，
∴AB=25cm，CE=CF=3cm，BE=BD，AF=AD，
∴设BE=x，则BD=x，AD=AF=25-x，
∴BC2+AC2=AB2，
∴（x+3）2+（3+25-x）2=252，
解得：x=4或21，
∴BE=4或21，
∴BC=4+3=7（cm）或3+21=24（cm），
则AC=3+21=24（cm）或3+4=7（cm），
故△ABC的三边长分别为：7cm，24cm，25cm．
∴AB=25cm，CE=CF=3cm，BE=BD，AF=AD，
∴设BE=x，则BD=x，AD=AF=25-x，
∴BC2+AC2=AB2，
∴（x+3）2+（3+25-x）2=252，
解得：x=4或21，
∴BE=4或21，
∴BC=4+3=7（cm）或3+21=24（cm），
则AC=3+21=24（cm）或3+4=7（cm），
故△ABC的三边长分别为：7cm，24cm，25cm．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
