Question

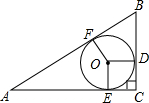
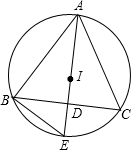
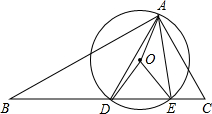
已知△ABC中，∠BAC=90°，点D，E在BC边上，且BA=BE，CA=CD，作△ADE的外接圆⊙O并连接OA、OD、OE．
（1）求证：BO平分∠ABC；
（2）求证：∠DAO=90°-∠AED；
（3）求∠DOE的度数．

Answer 1

（1）证明：∵OA=OE，BO=BO，BA=BE，
∴△OAB≌△OEB，
∴∠ABO=∠EBO．
即BO平分∠ABC．

（2）证明：∵∠DAO=

180°-∠AOD

2

，
∠AOD=2∠AED，
∴∠DAO=90°-∠AED．

（3）∵BA=BE，CA=CD，
∴∠BAE=∠BEA，∠CAD=∠CDA．
∴∠BEA=

180°-∠ABC

2

，∠CDA=

180°-∠ACB

2

．
∴∠BEA+∠CDA=180°-

1

2

（∠ABC+∠ACB）=135°．
∴∠DAE=45°，
∴∠DOE=90°．