题目内容
已知△ABC的内切圆⊙O如图,若∠DEF=54°,则∠BAC等于( )
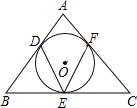
| A.96° | B.48° | C.24° | D.72° |

如图,连接OD、OE,则∠ODA=∠OFA=90°;
⊙O中,∠DOF=2∠DEF=2×54°=108°;
四边形ADEF中,∠ODA=∠OFA=90°,
∴∠BAC+∠DOF=180°,
即∠BAC=180°-∠DOF=72°.
故选D.
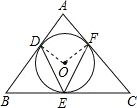
⊙O中,∠DOF=2∠DEF=2×54°=108°;
四边形ADEF中,∠ODA=∠OFA=90°,
∴∠BAC+∠DOF=180°,
即∠BAC=180°-∠DOF=72°.
故选D.


练习册系列答案
相关题目
