题目内容
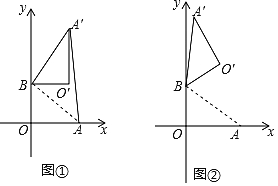
【题目】函数
与
的图象如图所示，有以下结论：①
；②
；③
；④当
时，
.其中正确的结论有（ ）
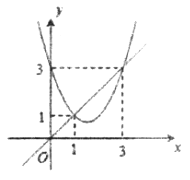
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
由函数y=x2+bx+c与x轴无交点，可得b2-4c＜0；当x=1时，y=1+b+c=1；当x=3时，y=9+3b+c=3；当1＜x＜3时，二次函数值小于一次函数值，可得x2+bx+c＜x，继而可求得答案．
①由图象可知：抛物线与x轴无交点，即△＜0，∴△=b2-4ac＜0，故此选项错误；
②由图象可知：抛物线过点(1，1)即当x=1时，y=a+b+c=1，
a+b+c+1=2>0，故此选项正确；
③由点(3，3)在抛物线上，得到9a+3b+c=3，
∴9a+3b+c+3=6>0，正确；
④由图象可知，当1＜x＜3时，抛物线在直线y=kx的下方，
即当1＜x＜3时，x2+bx+c＜kx，
∴x2+(b-k)x+c＜0，故此选项正确.
故选C.
练习册系列答案
相关题目
