题目内容
【题目】在平面直角坐标系中，O为原点，点A（4，0），点B（0，3），把△ABO绕点B逆时针旋转得到△A′BO′，点A、O旋转后的对应点为A′、O′，记旋转角为α．
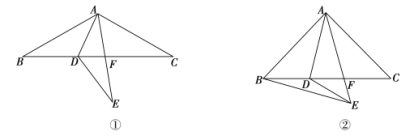
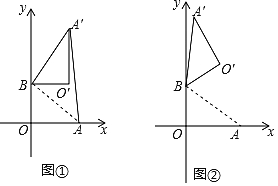
（1）如图①，若α=90°，求AA′的长；
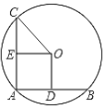
（2）如图②，若α=120°，求点O′的坐标；
（3）记K为AB的中点，S为△KA′O′的面积，求S的取值范围（直接写出结果即可）．
【答案】（1）5
（2）（
，
）（3）1≤S≤11
【解析】
（1）根据勾股定理得AB=5，由旋转性质可得∠A′BA=90°，A′B=AB=5，然后即可得出AA′=5；
（2）作O′C⊥y轴，由旋转是性质可得：∠O′BO=120°，O′B=OB=3，在Rt△O′CB中，由∠O′BC=60°得BC、O′C的长，即可得到答案；
（3）如图③中，当点O′在AB上时，△KA′O′的面积最小，当点O′在AB的延长线上时，△KA′O′的面积最大，求出面积的最小值以及最大值即可解决问题.
（1）如图①，∵点A（4，0），点B（0，3），
∴OA=4，OB=3．
在Rt△ABO中，由勾股定理得AB=5，
根据题意，△A′BO′是△ABO绕点B逆时针旋转90°得到的，
由旋转是性质可得：∠A′BA=90°，A′B=AB=5，
∴AA′=5；
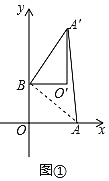
（2）如图②，根据题意，由旋转是性质可得：∠O′BO=120°，O′B=OB=3，
过点O′作O′C⊥y轴，垂足为C，则∠O′CB=90°，
在Rt△O′CB中，∵∠O′BC=60°，∠BO′C=30°，
∴BC=
O′B=
．
由勾股定理O′C=，
∴OC=OB+BC=，
∴点O′的坐标为（，）；
（3）如图③中，
当点O′在AB上时，△KA′O′的面积最小，最小面积=KO′×AO′=×（3-2.5）×4=1，
当点O′在AB的延长线上时，△KA′O′的面积最大，最大面积=×KO′×AO′=×（3+2.5）×4=11．
综上所述，1≤S≤11．
