题目内容
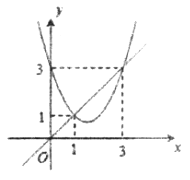
【题目】廊桥是我国古老的文化遗产，如图，是某座抛物线型的廊桥示意图.已知水面AB宽40米，抛物线最高点C到水面AB的距离为10米，为保护廊桥的安全，在该抛物线上距水面AB高为8米的点E，F处要安装两盏警示灯，求这两盏灯的水平距离EF.（结果保留根号）
【答案】
.
【解析】
利用待定系数法求得抛物线的解析式.已知抛物线上距水面AB高为8米的E、F两点,可知E、F两点纵坐标为8,把y=8代入抛物线解析式,可求E、F两点的横坐标,根据抛物线的对称性求EF长.
如图，以AB所在直线为x轴、线段AB的中垂线为y轴建立直角坐标系，
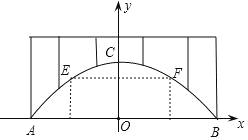
由题意知，A(20，0)，B(20，0)，C(0，10).
设过点A， B，C的抛物线方程为：y=a(x+20)(x20)(a<0).
把点C(0，10)的坐标代入，得
10=a(0+20)(020)，
解得：a=
，
则该抛物线的解析式为：y= (x+20)(x20)= x2+10，
把y=8代入,得x2+10=8，
即x2=80，
∴x1=4
，x2=4，
所以两盏警示灯之间的水平距离为：EF=|x1x2|=|4(4)|=8 (m).
【题目】在不透明的袋子中有四张标有数字1，2，3，4的卡片，小明、小华两人按照各自的规则玩抽卡片游戏。
小明画出树形图如下：
小华列出表格如下：
第一次 第二次 | 1 | 2 | 3 | 4 |
1 | （1，1） | （2，1） | （3，1） | （4，1） |
2 | （1，2） | （2，2） | ① | （4，2） |
3 | （1，3） | （2，3） | （3，3） | （4，3） |
4 | （1，4） | （2，4） | （3，4） | （4，4） |
回答下列问题：
（1）根据小明画出的树形图分析，他的游戏规则是：随机抽出一张卡片后 （填“放回”或“不放回”），再随机抽出一张卡片；
（2）根据小华的游戏规则，表格中①表示的有序数对为 ；
（3）规定两次抽到的数字之和为奇数的获胜，你认为淮获胜的可能性大？为什么？