题目内容
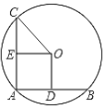
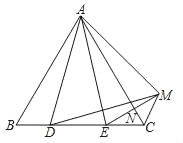
【题目】如图,△ABC是等边三角形,D,E是BC上的两点,且BD=CE,连接AD、AE,将△AEC沿AC翻折,得到△AMC,连接EM交AC于点N,连接DM.以下判断:①AD=AE,②△ABD≌△DCM,③△ADM是等边三角形,④CN=![]() EC中,正确的是_____.
EC中,正确的是_____.
【答案】①③④.
【解析】
由等边三角形的性质得出AB=AC,∠B=∠BAC=∠ACE=60![]() ,由SAS证得△ABD≌△ACE,得出∠BAD=∠CAE,AD=AE,由折叠的性质得CE=CM=BD,AE=AM=AD,∠CAE=∠CAM=∠BAD,推出∠DAM=∠BAC=60
,由SAS证得△ABD≌△ACE,得出∠BAD=∠CAE,AD=AE,由折叠的性质得CE=CM=BD,AE=AM=AD,∠CAE=∠CAM=∠BAD,推出∠DAM=∠BAC=60![]() ,则△ADM是等边三角形,得出DM=AD,易证AB>DM,AD>DC,得出△ABD与△DCM不全等,由折叠的性质得AE=AM,CE=CM,则AC垂直平分EM,即∠ENC=90
,则△ADM是等边三角形,得出DM=AD,易证AB>DM,AD>DC,得出△ABD与△DCM不全等,由折叠的性质得AE=AM,CE=CM,则AC垂直平分EM,即∠ENC=90![]() ,由∠ACE=60
,由∠ACE=60![]() ,得出∠CEN=30
,得出∠CEN=30![]() ,即可得出CN=
,即可得出CN=![]() EC.
EC.
解:∵△ABC是等边三角形,
∴AB=AC,∠B=∠BAC=∠ACE=60![]() ,
,
在△ABD和△ACE中,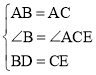 ,
,
∴△ABD≌△ACE(SAS),
∴∠BAD=∠CAE,AD=AE,故①正确;
由折叠的性质得:CE=CM=BD,AE=AM=AD,∠CAE=∠CAM=∠BAD,
∴∠DAM=∠BAC=60![]() ,
,
∴△ADM是等边三角形,
∴DM=AD,
∵AB>AD,
∴AB>DM,
∵∠ACD>∠DAC,
∴AD>DC,
∴△ABD与△DCM不全等,故③正确、②错误;
由折叠的性质得:AE=AM,CE=CM,
∴AC垂直平分EM,
∴∠ENC=90![]() ,
,
∵∠ACE=60![]() ,
,
∴∠CEN=30![]() ,
,
∴CN=![]() EC,故④正确,
EC,故④正确,
故答案为:①③④.

 科学实验活动册系列答案
科学实验活动册系列答案【题目】我们在学完“平移、轴对称、旋转”三种图形的变化后,可以进行进一步研究,请根据示例图形,完成下表.
图形的变化 | 示例图形 | 与对应线段有关的结论 | 与对应点有关的结论 |
平移 |
| (1)__________. |
|
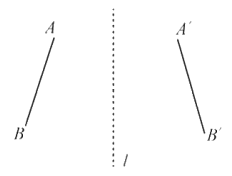
轴对称 |
| (2)__________. | (3)__________. |
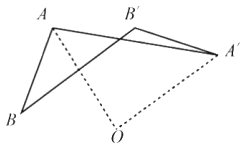
旋转 |
|
| (4)__________. |